Hướng dẫn giải Câu hỏi Luyện tập 1 trang 68 SGK Toán 9 Kết nối tri thức – Bài 11. Tỉ số lượng giác của góc nhọn. Hướng dẫn: Xét tam giác ABC vuông tại A, ta có.
Câu hỏi/Đề bài:
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Hướng dẫn:
Xét tam giác ABC vuông tại A, ta có:
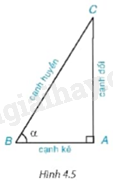
Tỉ số giữa cạnh đối và cạnh huyền gọi là sin của góc B, kí hiệu \(\sin \widehat B\)
Tỉ số giữa cạnh kề và cạnh huyền gọi là cosin của góc B, kí hiệu \(\cos \widehat B\)
Tỉ số giữa cạnh đối và cạnh kề của góc B gọi là \(\tan \widehat B\)
Tỉ số giữa cạnh kề và cạnh đối của góc B gọi là \(\cot \widehat B\)
Ở bài toán này ta còn thiếu cạnh huyền BC, do đó cần sử dụng định Pythagore để tính.
Lời giải:
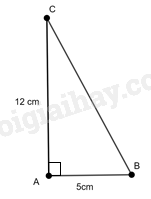
Xét tam giác ABC vuông tại A, ta có \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)
Nên \(B{C^2} = {5^2} + {12^2} = 169\) suy ra \(BC = 13\) (cm) .
Theo định nghĩa của tỉ số lượng giác ta có:
\(\sin \widehat B = \frac{{AC}}{{BC}} = \frac{{12}}{{13}};\\\cos \widehat B = \frac{{AB}}{{BC}} = \frac{5}{{13}};\\\tan \widehat B = \frac{{AC}}{{AB}} = \frac{{12}}{5};\\\cot \widehat B = \frac{{AB}}{{AC}} = \frac{5}{{12}}\)