Hướng dẫn giải Câu hỏi Hoạt động 1 trang 67 SGK Toán 9 Kết nối tri thức – Bài 11. Tỉ số lượng giác của góc nhọn. Tham khảo: Chứng minh tam giác đồng dạng theo trường hợp góc – góc (tam giác có hai cặp góc tương ứng.
Câu hỏi/Đề bài:
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B’} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A’B’C’;\)
b) \(\frac{{AC}}{{BC}} = \frac{{A’C’}}{{B’C’}};\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}};\frac{{AC}}{{AB}} = \frac{{A’C’}}{{A’B’}};\frac{{AB}}{{AC}} = \frac{{A’B’}}{{A’C’}}\)
Hướng dẫn:
Chứng minh tam giác đồng dạng theo trường hợp góc – góc (tam giác có hai cặp góc tương ứng bằng nhau) , sử dụng tính chất của tỉ lệ thức để chứng minh ý b (\(\frac{a}{b} = \frac{c}{d}\) suy ra \(\frac{a}{c} = \frac{b}{d}\) và \(\frac{b}{a} = \frac{d}{c}\) (tính chất tỉ lệ thức) ) .
Lời giải:
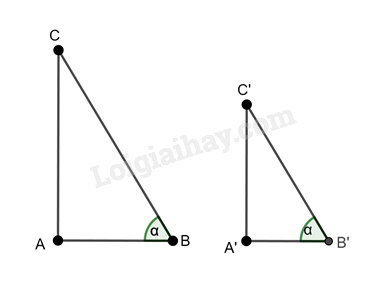
a) Xét hai tam giác ABC và tam giác A’B’C’ ta có:
\(\begin{array}{l}\widehat A = \widehat {A’} = {90^0}\\\widehat B = \widehat {B’} = \alpha \end{array}\)
Nên \(\Delta ABC\backsim \Delta A’B’C’\left( g-g \right)\)
b) \(\Delta ABC\backsim \Delta A’B’C’\) suy ra \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}} = \frac{{AC}}{{A’C’}}\) (tỉ lệ các cạnh tương ứng)
Do \(\frac{{AB}}{{A’B’}} = \frac{{BC}}{{B’C’}}\) nên ta có \(\frac{{AB}}{{BC}} = \frac{{A’B’}}{{B’C’}}\) (tính chất tỉ lệ thức)
Do \(\frac{{BC}}{{B’C’}} = \frac{{AC}}{{A’C’}}\) nên ta có \(\frac{{A’C’}}{{B’C’}} = \frac{{AC}}{{BC}}\) (tính chất tỉ lệ thức)
Do \(\frac{{AB}}{{A’B’}} = \frac{{AC}}{{A’C’}}\) nên ta có \(\frac{{AB}}{{AC}} = \frac{{A’B’}}{{A’C’}}\) và \(\frac{{AC}}{{AB}} = \frac{{A’B’}}{{A’C’}}\) (tính chất tỉ lệ thức)