Lời giải Câu hỏi Hoạt động 4 trang 102 SGK Toán 9 Kết nối tri thức – Bài 16. Vị trí tương đối của đường thẳng và đường tròn. Gợi ý: Chứng minh \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\), từ đó suy ra các cặp cạnh, góc tương ứng bằng nhau.
Câu hỏi/Đề bài:
(Dựa vào hình vẽ có được sau HĐ3).
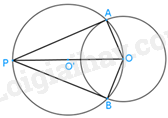
Bằng cách xét hai tam giác OPA và OPB, chứng minh rằng:
a) PA = PB;
b) PO là tia phân giác của góc APB;
c) OP là tia phân giác của góc AOB.
Hướng dẫn:
Chứng minh \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\), từ đó suy ra các cặp cạnh, góc tương ứng bằng nhau.
Lời giải:
a) Xét hai tam giác vuông OAP và OBP có:
OA = OB
OP chung
Vậy \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (cạnh huyền – cạnh góc vuông)
Suy ra: PA = PB (hai cạnh tương ứng)
b) Vì \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (câu a) nên \(\widehat {{\rm{OAP}}} = \widehat {{\rm{OBP}}}\) (hai góc tương ứng)
Suy ra PO là tia phân giác của góc APB.
c) Vì \(\Delta {\rm{OAP}} = \Delta {\rm{OBP}}\) (câu a) nên \(\widehat {{\rm{AOP}}} = \widehat {{\rm{BOP}}}\) (hai góc tương ứng)
Suy ra OP là tia phân giác của góc AOB.