Chứng minh \(\widehat {ABD} + \widehat {ACD} = {180^o}\), mà \(\widehat {ICA} + \widehat {ACD} = {180^o}\) nên \(\widehat {IBD} = \widehat {ICA}\). Giải và trình bày phương pháp giải Giải bài tập 9.19 trang 83 SGK Toán 9 tập 2 – Kết nối tri thức – Bài 29. Tứ giác nội tiếp. Cho điểm I nằm ngoài đường tròn (O)….
Đề bài/câu hỏi:
Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại bốn điểm A, B và C, D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng \(\widehat {IBD} = \widehat {ICA},\widehat {IAC} = \widehat {IDB}\) và \(IA.IB = IC.ID\).
Hướng dẫn:
+ Chứng minh \(\widehat {ABD} + \widehat {ACD} = {180^o}\), mà \(\widehat {ICA} + \widehat {ACD} = {180^o}\) nên \(\widehat {IBD} = \widehat {ICA}\).
+ Chứng minh \(\widehat {CAB} + \widehat {CDB} = {180^o}\), mà \(\widehat {CAB} + \widehat {IAC} = {180^o}\) nên \(\widehat {IAC} = \widehat {IDB}\).
+ Chứng minh $\Delta ICB\backsim \Delta IAD\Rightarrow \frac{IC}{IA}=\frac{IB}{ID}\Rightarrow IA.IB=IC.ID$
Lời giải:
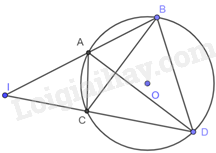
Tứ giác ABDC nội tiếp (O) nên \(\widehat {ABD} + \widehat {ACD} = {180^o}\), mà \(\widehat {ICA} + \widehat {ACD} = {180^o}\) (hai góc kề bù) nên \(\widehat {IBD} = \widehat {ICA}\)
Tứ giác ABDC nội tiếp (O) nên\(\widehat {CAB} + \widehat {CDB} = {180^o}\), mà \(\widehat {CAB} + \widehat {IAC} = {180^o}\) (hai góc kề bù) nên \(\widehat {IAC} = \widehat {IDB}\)
Tam giác ICB và tam giác IAD có:
Góc I chung, \(\widehat {IBC} = \widehat {IDA}\) (hai góc nội tiếp đường tròn (O) cùng chắn cung AC).
Do đo, $\Delta ICB\backsim \Delta IAD\Rightarrow \frac{IC}{IA}=\frac{IB}{ID}\Rightarrow IA.IB=IC.ID$.