Gọi H là hình chiếu của M trên AB. Khi đó khoảng cách từ M đến AB bằng độ dài đoạn MH. Lời giải Giải bài tập 5.5 trang 90 SGK Toán 9 tập 1 – Kết nối tri thức – Bài 14. Cung và dây của một đường tròn. Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó….
Đề bài/câu hỏi:
Cho nửa đường tròn đường kính AB và một điểm M tùy ý thuộc nửa đường tròn đó. Chứng minh rằng khoảng cách từ M đến AB không lớn hơn \(\frac{{AB}}{2}.\)
Hướng dẫn:
Gọi H là hình chiếu của M trên AB.
Khi đó khoảng cách từ M đến AB bằng độ dài đoạn MH.
Xét tam giác MHO vuông tại H có: \(MH \le MO = \frac{{AB
Lời giải:
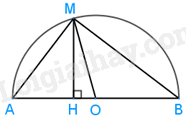
Gọi H là hình chiếu của M trên AB.
Khi đó khoảng cách từ M đến AB bằng độ dài đoạn MH.
Xét tam giác MHO vuông tại H có: \(MH \le MO\)
Lại có: \(MO = \frac{{AB}}{2}\)(do AB là đường kính, OM là bán kính của đường tròn (O)).
Vậy \(MH \le \frac{{AB}}{2}.\)