Giải Câu hỏi Hoạt động 3 trang 63 SGK Toán 9 Chân trời sáng tạo – Bài 1. Tỉ số lượng giác của góc nhọn. Hướng dẫn: Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \).
Câu hỏi/Đề bài:
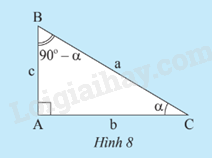
a) Tính các tỉ số lượng giác của góc \(\alpha \) và của góc 90o -\(\alpha \) trong Hình 8 theo a, b, c.
b) So sánh sin \(\widehat B\) và cos \(\widehat C\) , cos \(\widehat B\) và sin \(\widehat C\) , tan \(\widehat B\) và cot \(\widehat C\) , tan \(\widehat C\) và cot \(\widehat B\).
Hướng dẫn:
– Dựa vào tỉ số lượng giác của góc nhọn \(\alpha \). Xét tam giác ABC vuông tại A có \(\widehat {ACB} = \alpha \) , ta có:
+ Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc \(\alpha \) , kí hiệu sin\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc \(\alpha \) , kí hiệu cos\(\alpha \).
+ Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc \(\alpha \) , kí hiệu tan\(\alpha \).
+ Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc \(\alpha \) , kí hiệu cot\(\alpha \).
Lời giải:
Xét tam giác ABC vuông tại A. Ta có:
Các tỉ số lượng giác của góc \(\alpha \) là:
sin \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\)
cos \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\)
tan \(\alpha \) = \(\frac{{AB}}{{AC}} = \frac{c}{b}\)
cot \(\alpha \) = \(\frac{1}{{\tan \alpha }} = \frac{b}{c}\)
Các tỉ số lượng giác của góc 90o – \(\alpha \) là:
sin 90o – \(\alpha \) = \(\frac{{AC}}{{BC}} = \frac{b}{a}\)
cos 90o – \(\alpha \) = \(\frac{{AB}}{{BC}} = \frac{c}{a}\)
tan 90o – \(\alpha \) = \(\frac{{AC}}{{AB}} = \frac{b}{c}\)
cot 90o – \(\alpha \) = \(\frac{1}{{\tan {{90}^o} – \alpha }} = \frac{c}{b}\)
b) Ta có \(\widehat C\) = \(\alpha \) ; \(\widehat B\) = 90o – \(\alpha \) nên theo phần a ta có:
sin \(\widehat B\) = cos \(\widehat C\)
cos \(\widehat B\) = sin \(\widehat C\)
tan \(\widehat B\) = cot \(\widehat C\)
tan \(\widehat C\) = cot \(\widehat B\)