Đáp án Câu hỏi Luyện tập 5 trang 73 SGK Toán 9 Cánh diều – Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác. Hướng dẫn: Bước 1: Tính AM (dựa vào tính chất đường trung tuyến trong tam giác).
Câu hỏi/Đề bài:
Cho tam giác đều ABC ngoại tiếp đường tròn (O; 6). Tính AB.
Hướng dẫn:
Bước 1: Tính AM (dựa vào tính chất đường trung tuyến trong tam giác).
Bước 2: Tính BM theo AB.
Bước 3: Áp dụng Định lý Pytago trong tam giác vuông AMB.
Lời giải:
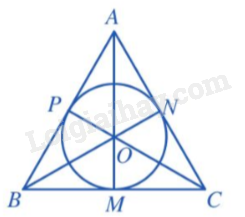
Giả sử tam giác ABC ngoại tiếp (O) với phân giác AM, suy ra AM đồng thời là đường trung tuyến.
Có đường tròn (O; 6) nên OM = 6.
Xét tam giác ABC đều có đường trung tuyến AM nên \(AM = 3OM = 3.6 = 18\) và \(BM = \frac{{BC}}{2} = \frac{{AB}}{2}\), đồng thời AM cũng là đường cao, do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác AMB vuông tại M có:
\(\begin{array}{l}A{M^2} + B{M^2} = A{B^2}(Pytago)\\A{M^2} + {\frac{{AB}}{4}^2} = A{B^2}\\{18^2} = {\frac{{3AB}}{4}^2}\\AB = 12\sqrt 3 \end{array}\)
Vậy \(AB = 12\sqrt 3 .\)