Giải Câu hỏi Hoạt động 7 trang 73 SGK Toán 9 Cánh diều – Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác. Hướng dẫn: Áp dụng: Trong tam giác cân, đường trung tuyến đồng thời là đường phân giác.
Câu hỏi/Đề bài:
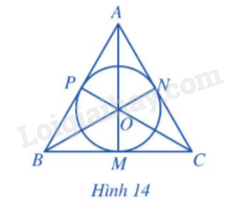
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 14).
a) AM, BN, CP có là các đường phân giác của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn nội tiếp tam giác ABC hay không?
c) Tính OM theo a.
Hướng dẫn:
a) Áp dụng: Trong tam giác cân, đường trung tuyến đồng thời là đường phân giác.
b) Chứng minh OM = ON = OP.
c) Áp dụng Pytago trong tam giác AMB vuông tại M.
Lời giải:
a) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP đồng thời là ba đường phân giác.
b) Do O là giao của 3 đường phân giác trong tam giác ABC nên O cách đều 3 cạnh của tam giác, do đó OM = ON = OP.
Vậy đường tròn (O) là đường tròn nội tiếp tam giác ABC.
c) Xét tam giác ABC đều có đường trung tuyến AM nên \(BM = \frac{{BC}}{2} = \frac{a}{2}\) và AM đồng thời là đường cao, do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác AMB vuông tại M có:
\(AM = \sqrt {A{B^2} – B{M^2}} \) (Pytago).
Nên \(AM = \sqrt {{a^2} – {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{\sqrt 3 a}}{2}.\)
Mà \(OM = \frac{1}{3}AM\)(do AM là đường trung tuyến trong tam giác ABC).
Suy ra \(OM = \frac{1}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{6}.\)