Trả lời Câu hỏi Luyện tập 3 trang 71 SGK Toán 9 Cánh diều – Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác. Gợi ý: Kẻ đường trung trực AH.
Câu hỏi/Đề bài:
Cho tam giác đều ABC nội tiếp đường tròn (O; 2cm). Tính AB.
Hướng dẫn:
Kẻ đường trung trực AH.
Áp dụng Định lý độ dài đường trung tuyến trong tam giác để tính AH.
Áp dụng Định lý Pytago để tính BH rồi tính AB.
Lời giải:
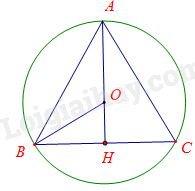
Chứng minh
Kẻ đường trung trực AH của tam giác ABC suy ra \(O \in AH,\widehat {OHB} = 90^\circ .\)
Vì tam giác đều ABC nội tiếp đường tròn (O; 2cm) nên OA = OB = 2cm.
Ta lại có: AH là đường trung trực của tam giác đều ABC nên AH đồng thời là đường trung tuyến, do đó \(OH = \frac{1}{2}AO = \frac{1}{2}.2 = 1cm,AH = 3OH = 3.1 = 3cm.\)
Xét tam giác OHB vuông tại H, áp dụng định lý Pytago ta có: \(BH = \sqrt {B{O^2} – O{H^2}} = \sqrt {{2^2} – {1^2}} = \sqrt 3 cm.\)
Xét tam giác AHB vuông tại H, áp dụng định lý Pytago ta có:
\(AB = \sqrt {{3^2} + {{\sqrt 3 }^2}} = 2\sqrt 3 cm.\)
Vậy\(AB = 2\sqrt 3 cm.\)