Giải Câu hỏi Hoạt động 4 trang 70 SGK Toán 9 Cánh diều – Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác. Tham khảo: Nhớ lại tính chất: Đường trung tuyến xuất phát từ đỉnh của tam giác cân cũng là đường trung.
Câu hỏi/Đề bài:
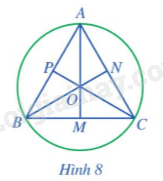
Cho tam giác đều ABC cạnh a, ba đường trung tuyến AM, BN, CP cắt nhau tại trọng tâm O (Hình 8).
a) AM, BN, CP có là các đường trung trực của tam giác ABC hay không?
b) Điểm O có là tâm đường tròn ngoại tiếp tam giác ABC hay không?
c) Tính AM theo a.
d) Tính OA theo a.
Hướng dẫn:
a) Nhớ lại tính chất: Đường trung tuyến xuất phát từ đỉnh của tam giác cân cũng là đường trung trực của tam giác đó.
b) Xét xem O có cách đều 3 đỉnh của tam giác hay không.
c) Tính BM, sau đó áp dụng định lý Pytago trong tam giác vuông AMB.
d) Áp dụng: khoảng cách từ trọng tâm tới đỉnh của tam giác bằng \(\frac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Lời giải:
a) Vì tam giác ABC đều nên ba đường trung tuyến AM, BN, CP cũng đồng thời là ba đường trung trực của tam giác ABC. Do đó AM, BN, CP lần lượt là trung trực của BC, AC, AB.
b) Do ba đường trung trực của tam giác ABC cắt nhau tại O nên O cách đều 3 đỉnh A, B, C (tính chất 3 đường trung trực của tam giác).
Vậy O là tâm đường tròn ngoại tiếp tam giác ABC.
c) Xét tam giác đều ABC cạnh a có trung tuyến AM nên \(BM = \frac{1}{2}BC = \frac{a}{2}.\)
AM là đường trung trực của tam giác ABC (cmt) nên \(AM \bot BC\) do đó \(\widehat {AMB} = 90^\circ .\)
Xét tam giác ABM vuông tại M có:
\(A{M^2} = A{B^2} – B{M^2} = {a^2} – {\left( {\frac{a}{2}} \right)^2} = \frac{{3{a^2}}}{4}\) (Pytago)
\(AM = \frac{{\sqrt 3 a}}{2}.\)
d) Ta có: AM là trung tuyến của tam giác ABC, O là trọng tâm nên \(OA = \frac{2}{3}AM = \frac{2}{3}.\frac{{\sqrt 3 a}}{2} = \frac{{\sqrt 3 a}}{3}.\)