Đáp án Câu hỏi Luyện tập 3 trang 108 SGK Toán 9 Cánh diều – Bài 3. Tiếp tuyến của đường tròn. Gợi ý: Dựa vào các kiến thức vừa học để chứng minh.
Câu hỏi/Đề bài:
Cho hai đường tròn \(\left( O \right),\left( {O’} \right)\) cắt nhau tại hai điểm \(A,B\) sao cho đường thẳng \(OA\) là tiếp tuyến của đường tròn \(\left( {O’} \right)\). Chứng minh đường thẳng \(O’B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Hướng dẫn:
Dựa vào các kiến thức vừa học để chứng minh.
Lời giải:
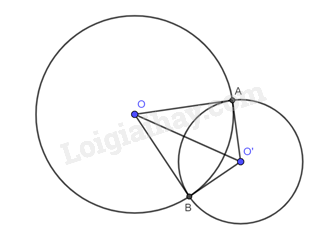
Do \(OA\) là tiếp tuyến của đường tròn \(\left( {O’} \right)\) nên \(O’A \bot OA\). Vậy \(\widehat {OAO’} = 90^\circ \).
Xét tam giác \(OAO’\) và tam giác \(OBO’\) có:
\(\left\{ \begin{array}{l}O’A = O’B\\OO’\,\,chung\\OA = OB\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \Delta OAO’ = \Delta OBO’\left( {c.c.c} \right)\\ \Rightarrow \widehat {OAO’} = \widehat {OBO’}\end{array}\).
Mà \(\widehat {OAO’} = 90^\circ \) nên \(\widehat {OBO’} = 90^\circ \) hay \(OB \bot O’B\).
Vậy đường thẳng \(O’B\) là tiếp tuyến của đường tròn \(\left( O \right)\).