Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán. Hướng dẫn giải Giải bài tập 5 trang 87 SGK Toán 9 tập 1 – Cánh diều – Bài 2. Một số hệ thức về cạnh và góc trong tam giác vuông. Trong Hình 24, cho (widehat O = alpha ,AB = m) và (widehat {OAB} = widehat {OCA} = widehat {ODC}…
Đề bài/câu hỏi:
Trong Hình 24, cho \(\widehat O = \alpha ,AB = m\) và \(\widehat {OAB} = \widehat {OCA} = \widehat {ODC} = 90^\circ \).
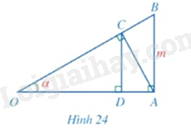
Chứng minh:
a) \(OA = m.\cot \alpha \);
b) \(AC = m.\cos \alpha \);
c) \(CD = m.{\cos ^2}\alpha \).
Hướng dẫn:
Dựa vào các mối liên hệ giữa tỉ số lượng giác và các cạnh để giải bài toán.
Lời giải:
a) Xét tam giác \(OAB\) vuông tại \(A\) ta có: \(OA = m.\cot \alpha \).
b) Xét tam giác \(OAC\) vuông tại \(C\) ta có:
\(AC = OA.\sin \alpha = m.\cot \alpha .\sin \alpha = m.\frac{{\cos \alpha }}{{\sin \alpha }}.\sin \alpha = m.\cos \alpha \).
c) Xét tam giác \(OAC\) vuông tại \(C\) ta có:
\(OC = OA.\cos \alpha = m.\cot \alpha .\cos \alpha = m.\frac{{\cos \alpha }}{{\sin \alpha }}.\cos \alpha = m.\frac{{{{\cos }^2}\alpha }}{{\sin \alpha }}\).
Xét tam giác \(OCD\) vuông tại \(D\) ta có:
\(CD = OC.\sin \alpha = m.\frac{{{{\cos }^2}\alpha }}{{\sin \alpha }}.\sin \alpha = m.{\cos ^2}\alpha \).