Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\). Thể tích của hình trụ: \(V = \pi {R^2}h\). Lời giải Giải bài 27 trang 135 sách bài tập toán 9 – Cánh diều tập 2 – Bài 3. Hình cầu. Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ với các kích thước như ở…
Đề bài/câu hỏi:
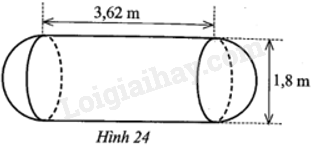
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ với các kích thước như ở Hình 24. Hỏi thể tích của bồn chứa bằng bao nhiêu mét khối (làm tròn kết quả đến hàng phần mười)?
Hướng dẫn:
Dựa vào: Thể tích của hình cầu: \(V = \frac{4}{3}\pi {R^3}\).
Thể tích của hình trụ: \(V = \pi {R^2}h\).
Lời giải:
Ta có bán kính hình cầu và bán kính đáy hình trụ đều là: 1,8 : 2 = 0,9 (m).
Tổng thể tích của hai nửa hình cầu chính là thể tích của một hình cầu có cùng bán kính và bằng: \(\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi .{(0,9)^3} = 0,972\pi \) (m3).
Thể tích phần hình trụ là:
V = πR2h = π.(0,9)2.3,62 = 2,9322π (m3).
Thể tích của bồn chứa là:
0,972π + 2,9322π = 3,9042π ≈ 3,9042.3,14 ≈ 12,3 (m3).