Bước 1: Áp dụng công thức \(s = vt\) để tính quãng đường PA, BA. Bước 2. Phân tích, đưa ra lời giải Giải bài 23 trang 88 sách bài tập toán 9 – Cánh diều tập 1 – Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn. Một thuyền đi với tốc độ 20km/h theo hướng Đông trong 1 giờ 30 phút từ vị trí P đến…
Đề bài/câu hỏi:
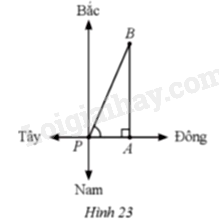
Một thuyền đi với tốc độ 20km/h theo hướng Đông trong 1 giờ 30 phút từ vị trí P đến vị trí A. Sau đó nó sẽ đi theo hướng Bắc với cùng tốc độ trong 3 giờ 30 phút đến vị trí B (Hình 23). Tính góc so với hướng Đông mà thuyền đi từ vị trí P đến vị trí B (làm tròn kết quả đến hàng đơn vị của phút).
Hướng dẫn:
Bước 1: Áp dụng công thức \(s = vt\) để tính quãng đường PA, BA.
Bước 2: Áp dụng tỉ số lượng giác trong tam giác PAB để tính góc B.
Lời giải:
Đổi 1 giờ 30 phút = 1,5h; 3 giờ 30 phút = 3,5h
Quãng đường PA là \(20.1,5 = 30\)km.
Quãng đường AB là \(20.3,5 = 70\)km.
Góc so với hướng Đông mà thuyền đi từ vị trí P đến vị trí B là góc APB.
Xét tam giác APB vuông tại A, ta có \(\tan \widehat {APB} = \frac{{BA}}{{PA}} = \frac{{70}}{{30}} = \frac{7}{3}\).
Do đó \(\widehat {APB} \approx 66^\circ 48’\).
Vậy góc cần tìm có số đo \(66^\circ 48’\).