Bước 1: Áp dụng tỉ số lượng giác trong 2 tam giác HMA và HMB để tính HA, HB. Bước 2. Vận dụng kiến thức giải Giải bài 24 trang 89 sách bài tập toán 9 – Cánh diều tập 1 – Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn. Từ một máy bay trực thăng, một người đặt mắt tại vị trí M ở độ cao MH = 920…
Đề bài/câu hỏi:
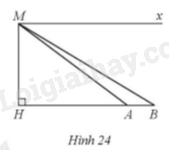
Từ một máy bay trực thăng, một người đặt mắt tại vị trí M ở độ cao MH = 920 m. Người đó nhìn hai vị trí A và B của hai đầu một cây cầu theo phương MA và MB tạo với phương nằm ngang Mx các góc lần lượt là \(\widehat {AMx} = 37^\circ ,\widehat {BMx} = 31^\circ \)với Mx // AB (Hình 24). Hỏi độ dài AB của cây cầu là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Hướng dẫn:
Bước 1: Áp dụng tỉ số lượng giác trong 2 tam giác HMA và HMB để tính HA, HB.
Bước 2: \(AB = HB – HA\).
Lời giải:
Do Mx // AB nên \(\widehat {AMx} = \widehat {MAH} = 37^\circ \), \(\widehat {BMx} = \widehat {MBH} = 31^\circ \) (các cặp góc so le trong).
Xét tam giác MAH vuông tại H ta có:
\(\tan \widehat {MAH} = \frac{{MH}}{{AH}}\) hay \(AH = \frac{{MH}}{{\tan \widehat {MAH}}} = \frac{{920}}{{\tan 37^\circ }}\)
Xét tam giác MBH vuông tại H ta có:
\(\tan \widehat {MBH} = \frac{{MH}}{{BH}}\) hay \(BH = \frac{{MH}}{{\tan \widehat {MBH}}} = \frac{{920}}{{\tan 31^\circ }}\)
Độ dài AB của cây cầu là:
\(AB = HB – HA = \frac{{920}}{{\tan 31^\circ }} – \frac{{920}}{{\tan 37^\circ }} \approx 310\)m.