Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O. Phân tích, đưa ra lời giải Giải bài 21 trang 113 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Phép quay. Cho điểm O cố định và số đo α° (0° < α° < 180°). a) Ở Hình 20,…
Đề bài/câu hỏi:
Cho điểm O cố định và số đo α° (0° < α° < 180°).
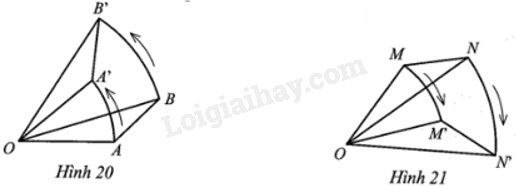
a) Ở Hình 20, phép quay ngược chiều α° tâm O biến điểm A thành điểm A’ và biến điểm B thành điểm B’. Chứng minh AB = A’B’.
b) Ở Hình 21, phép quay thuận chiều α° tâm O biến điểm M thành điểm M’ và biến điểm N thành điểm N’. Hỏi MN có bằng M’N’ hay không? Vì sao?
Hướng dẫn:
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\).
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên.
Lời giải:
a) Vì phép quay ngược chiều α° tâm O biến điểm A thành điểm A’ nên OA = OA’ và \(\widehat {AOA’} = {\alpha ^o}\).
Vì phép quay ngược chiều α° tâm O biến điểm B thành điểm B’ nên OB = OB’ và \(\widehat {BOB’} = {\alpha ^o}\).
Ta có \(\widehat {AOB} = \widehat {AOA’} – \widehat {A’OB} = {\alpha ^o} – \widehat {A’OB};\widehat {A’OB’} = \widehat {BOB’} – \widehat {A’OB} = {\alpha ^o} – \widehat {A’OB}\).
Suy ra \(\widehat {AOB} = \widehat {A’OB’}\).
Xét ∆OAB và ∆OA’B’ có:
OA = OA’, \(\widehat {AOB} = \widehat {A’OB’}\), OB = OB’
Do đó ∆OAB = ∆OA’B’ (c.g.c)
Suy ra AB = A’B’ (hai cạnh tương ứng).
b) Vì phép quay thuận chiều α° tâm O biến điểm M thành điểm M’ nên OM = OM’ và \(\widehat {MOM’} = {\alpha ^o}\).
Vì phép quay thuận chiều α° tâm O biến điểm N thành điểm N’ nên ON = ON’ và \(\widehat {NON’} = {\alpha ^o}\).
Ta có :
\(\widehat {MON} = \widehat {MOM’} – \widehat {NOM’} = {\alpha ^o} – \widehat {NOM’};\widehat {M’ON’} = \widehat {NON’} – \widehat {NOM’} = {\alpha ^o} – \widehat {NOM’}.\)
Suy ra \(\widehat {MON} = \widehat {M’ON’}\).
Xét ∆OMN và ∆OM’N’ có:
OM = OM’, \(\widehat {MON} = \widehat {M’ON’}\), ON = ON’
Do đó ∆OMN = ∆OM’N (c.g.c)
Suy ra MN = M’N’ (hai cạnh tương ứng).