Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O. Phân tích và giải Giải bài 20 trang 112 sách bài tập toán 9 – Cánh diều tập 2 – Bài 2. Phép quay. Cho hình đa giác đều có 9 cạnh ABCDEFGHI với tâm O (Hình 19). Tìm phát biểu sai,…
Đề bài/câu hỏi:
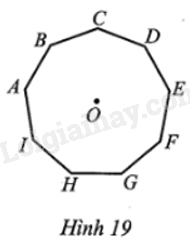
Cho hình đa giác đều có 9 cạnh ABCDEFGHI với tâm O (Hình 19). Tìm phát biểu sai, phát biểu đúng trong các phát biểu sau:
a) Các phép quay thuận chiều α° tâm O, với α° lần lượt nhận các giá trị 40°; 80°; …; 320°; 360° giữ nguyên hình đa giác đều ABCDEFGHI .
b) Phép quay ngược chiều 80° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm H, I, E, B, C.
c) Phép quay ngược chiều 120° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm G, H, I, A, C.
Hướng dẫn:
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\).
Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên.
Lời giải:
– Phát biểu a) đúng.
– Vì phép quay ngược chiều 80° tâm O biến điểm C thành điểm A nên phát biểu phép quay ngược chiều 80° tâm O biến điểm C thành điểm E là sai. Vậy phát biểu b) sai.
– Vì phép quay ngược chiều 120° tâm O biến điểm E thành điểm B nên phát biểu phép quay ngược chiều 120° tâm O biến điểm E thành điểm C là sai. Vậy phát biểu c) sai.