Bài 14 trang 14 SBT toán 9 – Cánh diều tập 1: Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m)

Đề bài/câu hỏi:

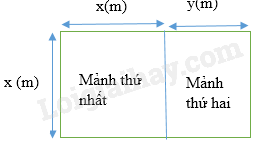
Người ta chia một khu đất có dạng hình chữ nhật thành hai mảnh: mảnh đất thứ nhất có dạng hình vuông với độ dài cạnh x (m); mảnh đất thứ hai có dạng hình chữ nhật với chiều dài x (m) và chiều rộng y (m) (x > y > 0) được minh hoạ ở Hình 3. Chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6.8 m. Trên một cạnh là chiều dài của khu đất, người ta đã xây một tường rào với chi phí 1 130 000 đồng theo giá 50000 đồng một mét.

a) Viết hệ hai phương trình bậc nhất hai ấn x, y biểu thị mối quan hệ giữa các đại lưọng.

b) Cặp số (13 ; 9,6) có phải là nghiệm của hệ phương trình ở câu a hay không? Vì sao?

Hướng dẫn:

a) Bước 1: Viết phương trình biểu diễn chu vi của cả khu đất.

Bước 2: Viết phương trình biểu diễn chi phí xây tường rào.

b) Thay cặp số (13; 9,6) vào từng phương trình, nếu kết quả của vế trái ở mỗi phương trình bằng vế phải của phương trình đó thì cặp số đó là nghiệm của hệ phương trình.

Lời giải:

a) Chu vi mảnh đất thứ nhất và mảnh đất thứ 2 lần lượt là \(4x(m)\) và \(2(x + y)(m)\).

Do chu vi của mảnh đất thứ nhất lớn hơn chu vi của mảnh đất thứ hai là 6.8 m nên ta có phương trình \(4x – 2(x + y) = 6,8\) hay \(x – y = 3,4\). (1)

Chiều dài cạnh của khu đất là \(x + y(m)\).

Trên cạnh đó, người ta xây một tường rào với chi phí 1 130 000 đồng theo giá 50000 đồng một mét nên ta có phương trình \(50000(x + y) = 1130000\) hay \(x + y = 22,6.\) (2)

Từ (1) và (2) ta có hệ phương trình \(\left\{ \begin{array}{l}x – y = 3,4\\x + y = 22,6\end{array} \right.\)

b) Thay x = 13; y = 9,6 vào từng phương trình \(x – y = 3,4\) trong hệ, ta có:

\(13 – 9,6 = 3,4\) và \(13 + 9,6 = 22,6\)

Vậy hệ phương trình trên nhận cặp số (13; 9,6) làm nghiệm.