Sử dụng công thức tính thể tích khối lập phương. Hướng dẫn giải Giải bài 8 trang 32 vở thực hành Toán 8 – Bài 7. Lập phương của một tổng. Lập phương của một hiệu. Từ một khối lập phương có độ dài cạnh là \(2x + 3\) (cm),…
Đề bài/câu hỏi:
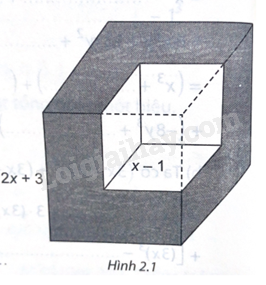
Từ một khối lập phương có độ dài cạnh là \(2x + 3\) (cm), ta cắt bỏ một khối lập phương có độ dài \(x-1\) (cm) (H.2.1). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.
Hướng dẫn:
Sử dụng công thức tính thể tích khối lập phương.
Lời giải:
Do cạnh của khối lập phương ban đầu là \(2x + 3\) nên thể tích của khối lập phương ban đầu là \({\left( {2x + 3} \right)^3}\).
Thể tích của khối lập phương bị cắt đi là \({\left( {x-1} \right)^3}\).
Thể tích phần còn lại là \({\left( {2x + 1} \right)^3} – {\left( {x – 1} \right)^3}\)
\(\begin{array}{l} = \left[ {{{\left( {2x} \right)}^3} + 3.{{\left( {2x} \right)}^2}.1 + 3.2x{{.1}^2} + {1^3}} \right] – \left( {{x^3} – 3{x^2} + 3x – 1} \right)\\ = 8{x^3} + 12{x^2} + 6x + 1 – {x^3} + 3{x^2} – 3x + 1\\ = \left( {8{x^3} – {x^3}} \right) + \left( {12{x^2} + 3{x^2}} \right) + \left( {6x – 3x} \right) + \left( {1 + 1} \right)\\ = 7{x^3} + 15{x^2} + 3x + 2.\end{array}\)