Trả lời Hoạt động 1 Bài 37. Hình đồng dạng (trang 104, 105, 106, 107) – SGK Toán 8 Kết nối tri thức. Tham khảo: Vì ΔOA’B’ ∽ ΔOAB (c. g. c) và ΔOB’C’ ∽ ΔOBC(c. g. c) nên ΔABC ∽ ΔA’B’C’ (c. g.
Câu hỏi/Đề bài:
Lấy điểm O và vẽ tam giác A’B’C’ như Hình 9.58. Trên các tia OA’, OB’, OC’, lấy các điểm A, B, C sao cho OA = 2OA’, OB = 2OB’, OC = 2OC’
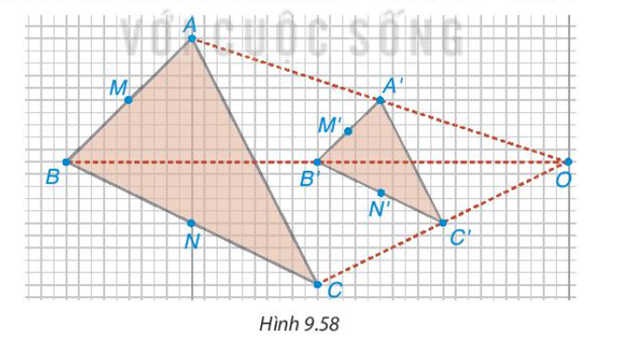
– Hãy giải thích vì sao ΔABC ∽ ΔA’B’C’ với tỉ số đồng dạng bằng 2
– Dùng thước thẳng, em hãy kiểm tra xem đường thẳng MM’, NN’ nối các trung điểm có đi qua O không?
Trong Hình 9.58, ta nói tam giác ABC là hình phóng to (2 lần) của tam giác A’B’C’ và tam giác A’B’C’ là hình thu nhỏ (2 lần) của tam giác ABC
Hướng dẫn:
Vì ΔOA’B’ ∽ ΔOAB (c.g.c) và ΔOB’C’ ∽ ΔOBC(c.g.c) nên ΔABC ∽ ΔA’B’C’ (c.g.c)
Lời giải:
– Có \(\frac{{OA’}}{{OA}} = \frac{{OB’}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOA’B’ ∽ ΔOAB (c.g.c)
– Có \(\frac{{OC’}}{{OC}} = \frac{{OB’}}{{OB}} = \frac{1}{2}\), góc O chung
=> ΔOB’C’ ∽ ΔOBC(c.g.c)
=> ΔABC ∽ ΔA’B’C’ (c.g.c)
– Đường thẳng có đi qua O