Hướng dẫn giải Hoạt động 5 Bài 1. Định lí Thalès trong tam giác (trang 46, 47, 48, 49) – SGK Toán 8 Chân trời sáng tạo. Tham khảo: Sử dụng Định lí Thales.
Câu hỏi/Đề bài:
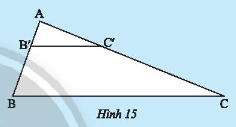
Cho tam giác \(ABC\) có \(AB = 6cm,AC = 15cm\). Trên \(AB,AC\) lần lượt lấy \(B’,C’\) sao cho \(AB’ = 2cm;AC’ = 5cm\).
a) Tính các tỉ số \(\frac{{AB’}}{{AB}}\) và \(\frac{{AC’}}{{AC}}\).
b) Qua \(B’\) vẽ đường thẳng song song với \(BC\) cắt \(AC\) tại \(E\). Tính \(AE\).
c) So sánh \(AE\) và \(AC’\).
d) Hãy nhận xét về vị trí của \(E\) và \(C’\), vị trí của hai đường thẳng \(B’C’\) và \(B’E\).
Hướng dẫn:
– Sử dụng Định lí Thales
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ.
Lời giải:
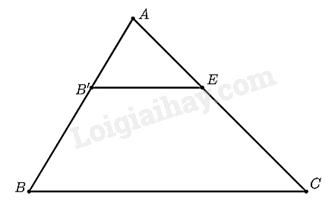
a) Ta có:
\(\frac{{AB’}}{{AB}} = \frac{2}{6} = \frac{1}{3}\) và \(\frac{{AC’}}{{AC}} = \frac{5}{{15}} = \frac{1}{3}\).
b) Vì \(B’E//BC\) và\(B’E\) cắt \(AC\) tại \(E\) nên theo định lí Thales ta có:
\(\frac{{AB’}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AE}}{{15}} \Rightarrow AE = \frac{{2.15}}{6} = 5cm\)
c) Ta có: \(AE = AC’ = 5cm\).
d) Điểm \(E \equiv C’\) và đường thẳng \(B’C’ \equiv B’E\).