Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới. Phân tích và giải Giải bài 3 trang 50 SGK Toán 8 tập 2- Chân trời sáng tạo – Bài 1. Định lí Thalès trong tam giác. Với số liệu được ghi trên Hình 21…
Đề bài/câu hỏi:
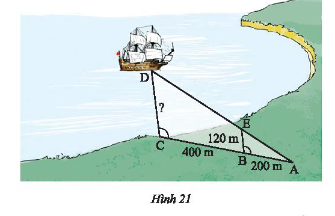
Với số liệu được ghi trên Hình 21. Hãy tính khoảng cách \(CD\) từ con tàu đến trạm quan trắc đặt tại điểm \(C\).
Hướng dẫn:
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Lời giải:
Ta có \(\widehat {ABE} = \widehat {ACD}\), mà hai góc này ở vị trí đồng vị nên \(BE//CD\).
Ta có: \(AC = AB + BC = 200 + 400 = 600m\)
Xét tam giác \(ACD\) có \(BE//CD\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AB}}{{AC}} = \frac{{BE}}{{CD}} \Rightarrow \frac{{200}}{{600}} = \frac{{120}}{{CD}}\). Do đó, \(CD = \frac{{120.600}}{{200}} = 360\).
Vậy \(CD = 360m\).