Áp dụng công thức tính thể tích của hình chóp tứ giác đều \(V = \frac{1}{3}. S. h\. Hướng dẫn giải Giải bài 26 trang 80 sách bài tập toán 8 – Cánh diều – Bài tập cuối Chương 4. Hình 17 mô tả một khối bê tông mác 200 dùng trong việc xây cầu….
Đề bài/câu hỏi:
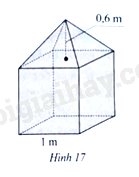
Hình 17 mô tả một khối bê tông mác 200 dùng trong việc xây cầu. Khối bê tông đó gồm hai phần: phần dưới có dạng hình lập phương với độ dài cạnh bằng 1 m, phần trên có dạng hình chóp tứ giác đều với chiều cao bằng 0,6 m. Cần phải chuẩn bị bao nhiêu tấn xi măng và bao nhiêu mét khối nước để làm khối bê tông đó? Biết rằng 1 m3 bê tông mác 200 cần khoảng 350,55 kg xi măng và 185 lít nước.
Hướng dẫn:
Áp dụng công thức tính thể tích của hình chóp tứ giác đều \(V = \frac{1}{3}.S.h\) và công thức tính thể tích của hình lập phương \(V = {a^3}\).
Lời giải:
Thể tích của phần dưới khối bê tông là: \({1^3} = 1\left( {{m^3}} \right)\)
Thể tích của phần trên khối bê tông là: \(\frac{1}{3}{.1^2}.0,6 = 0,2\left( {{m^3}} \right)\)
Thể tích của khối bê tông là: \(1 + 0,2 = 1,2\left( {{m^3}} \right)\)
Đổi 350,55 kg = 0,35055 tấn; 185 lít = 0,185 \({m^3}\)
Khối lượng xi măng cần dùng để làm khối bê tông đó là:
\(1,2.0,35055 = 0,42066\) (tấn)
Lượng nước cần dùng để làm khối bê tông đó là:
\(1,2.0,185 = 0,222\left( {{m^3}} \right)\).