Áp dụng công thức \(V = \frac{1}{3}. S. h\), trong đó \(V\) là thể tích \(S\) là diện tích đáy, \(h\. Vận dụng kiến thức giải Giải bài 25 trang 79 sách bài tập toán 8 – Cánh diều – Bài tập cuối Chương 4. Cho hai hình chóp đều \(A.BCDE\) và \(F.BCDE\) lần lượt có chiều cao là \(AO\) và \(FO\) (Hình 16)….
Đề bài/câu hỏi:
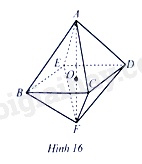
Cho hai hình chóp đều \(A.BCDE\) và \(F.BCDE\) lần lượt có chiều cao là \(AO\) và \(FO\) (Hình 16). Tính tỉ số thể tích của hình chóp tứ giác đều \(A.BCDE\) và \(F.BCDE\) biết \(FO = k.AO\left( {k > 0} \right)\).
Hướng dẫn:
Áp dụng công thức \(V = \frac{1}{3}.S.h\), trong đó \(V\) là thể tích \(S\) là diện tích đáy, \(h\) là chiều cao của hình chóp tứ giác đều.
Lời giải:
Thể tích của hình chóp tứ giác đều \(A.BCDE\) là: \(\frac{1}{3}.B{C^2}.AO\)
Thể tích của hình chóp tứ giác đều \(F.BCDE\) là:
\(\frac{1}{3}.B{C^2}.FO = \frac{1}{3}.B{C^2}.k.AO = k.\frac{1}{3}.B{C^2}.AO\)
Vậy tỉ số thể tích của hình chóp tứ giác đều \(A.BCDE\) và \(F.BCDE\) là \(\frac{1}{k}\).