Bài 1 trang 87 SBT toán 8 – Cánh diều: Tính độ dài x, y, z ở các hình 3a, 3b, 3c, 3d (độ dài ở các hình là cùng đơn vị đo)

Đề bài/câu hỏi:

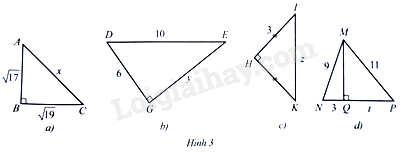
Tính độ dài \(x,y,z\) ở các hình \(3a,3b,3c,3d\) (độ dài ở các hình là cùng đơn vị đo):

Hướng dẫn:

Áp dụng định lí Pythagore trong tam giác vuông: Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Lời giải:

Áp dụng định lí Pythagore, ta có:

a) \(A{C^2} = A{B^2} + B{C^2}\), suy ra \({x^2} = {\left( {\sqrt {17} } \right)^2} + {\left( {\sqrt {19} } \right)^2} = 36\)

Vậy \(x = 6\)

b) \(D{E^2} = D{G^2} + G{E^2}\), suy ra \({10^2} = {6^2} + {y^2}\)

Vậy \(y = 8\)

c) \(I{K^2} = H{I^2} + H{K^2}\), suy ra \({z^2} = {3^2} + {3^2}\)

Vậy \(z = \sqrt {18} \)

d) Do tam giác \(MNQ\) vuông tại \(Q\) nên theo định lí Pythagore ta cóL

\(M{N^2} = M{Q^2} + N{Q^2}\). Suy ra \(M{Q^2} = M{N^2} – N{Q^2}\). Do đó, \(M{Q^2} = {9^2} – {3^2} = 72\)

Do tam giác \(MNQ\) vuông tại \(Q\) nên theo định lí Pythagore ta có:

\(M{P^2} = M{Q^2} + P{Q^2}\). Suy ra \(P{Q^2} = M{P^2} – M{Q^2}\). Do đó \({t^2} = {11^2} – 72 = 49\)

Vậy \(t = \sqrt {49} = 7\).