Giải Hoạt động 1 Bài 1. Góc và cạnh của một tam giác (trang 44, 45) – SGK Toán 7 Chân trời sáng tạo. Hướng dẫn: Ta dùng thước đo độ đo 3 góc của tam giác rồi tính tổng số đo của ba góc.
Câu hỏi/Đề bài:
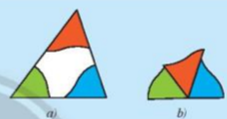
a) Cắt một tấm bìa hình tam giác và tô màu ba góc của nó (Hình 1a). Cắt rời ba góc ra khỏi tam giác rồi đặt ba góc kề nhau (Hình 1b).
Em hãy dự đoán tổng số đo ba góc trong Hình 1b.
b) Chứng minh tính chất về tổng số đo ba góc trong một tam giác theo gợi ý sau:
|
GT |
\(\Delta{ABC}\) |
|
KL |
\(\widehat A\)+\(\widehat B\)+\(\widehat C\)\( = {180^o}\) |
Qua A kẻ đường thẳng xy song song với BC như Hình 1c.
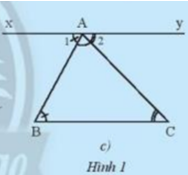
Ta có: xy // BC \( \Rightarrow \)\(\widehat B\)= ? (so le trong) (1)
và \(\widehat C\)= ? (so le trong) (2)
Từ (1) và (2) suy ra: \(\widehat B\)+\(\widehat {BAC}\)+\(\widehat C\)= \(\widehat {{A_1}}\)+\(\widehat {BAC}\)+\(\widehat {{A_2}}\)=\(\widehat {xAy}\)= ?
Hướng dẫn:
a) Ta dùng thước đo độ đo 3 góc của tam giác rồi tính tổng số đo của ba góc đó
Lời giải:
a) Ta dự đoán được sau khi ghép 3 góc nhọn đó sau khi ghép lại có tổng là \({180^o}\)
b) Qua A kẻ đường thẳng xy song song với BC
Ta có: xy // BC \( \Rightarrow \) \(\widehat B\) = \(\widehat {{A_1}}\) ( so le trong )
và \(\widehat C\) = \(\widehat {{A_2}}\)( so le trong )
Mà \(\widehat {{A_1}} + \widehat {BAC} + \widehat {{A_2}} = {180^o}\)
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \) Tổng 3 góc trong 1 tam giác = \({180^o}\)