Trả lời Hoạt động 2 Bài 9. Đường trung trực của một đoạn thẳng (trang 101, 102) – SGK Toán 7 Cánh diều. Gợi ý: Chứng minh \(\Delta MOA = \Delta MOB\)theo trường hợp c. g. c.
Câu hỏi/Đề bài:
Cho đoạn thẳng AB có trung điểm O, d là đường trung trực của đoạn thẳng AB, điểm M thuộc d, M khác O (Hình 90).
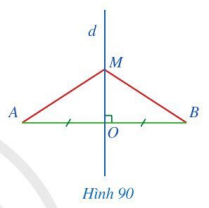
Chứng minh rằng:
a) \(\Delta MOA = \Delta MOB\);
b) MA = MB.
Hướng dẫn:
a) Chứng minh \(\Delta MOA = \Delta MOB\)theo trường hợp c.g.c.
b) Dựa vào kết quả của phần a) để chứng minh MA = MB.
Lời giải:
a) Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)