Chứng minh AB // CD bằng cách dựa vào đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD. Lời giải bài tập, câu hỏi Giải bài 2 trang 103 SGK Toán 7 tập 2 – Cánh diều – Bài 9. Đường trung trực của một đoạn thẳng. Trong Hình 95, đường thẳng a là đường trung trực của hai đoạn thẳng AB và CD. Chứng minh:…
Đề bài/câu hỏi:
Trong Hình 95, đường thẳng a là đường trung trực của hai đoạn thẳng AB và CD. Chứng minh:
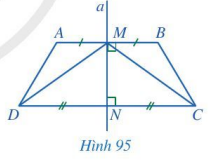
a) AB // CD;
b) \(\Delta MNC = \Delta MND;\)
c) \(\widehat {AMD} = \widehat {BMC}\);
d) \(AD = BC,\widehat A = \widehat B\);
e) \(\widehat {ADC} = \widehat {BCD}\).
Hướng dẫn:
a) Chứng minh AB // CD bằng cách dựa vào đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD.
b) Chứng minh \(\Delta MNC = \Delta MND\) theo trường hợp cạnh huyền – cạnh góc vuông.
c) Dựa vào kết quả của phần b) để chứng minh \(\widehat {AMD} = \widehat {BMC}\).
d) Chứng minh \(AD = BC,\widehat A = \widehat B\) dựa vào cách chứng minh \(\Delta MAD = \Delta MBC\).
e) Chứng minh \(\widehat {ADC} = \widehat {BCD}\) dựa vào kết quả của phần d).
Lời giải:
a) Ta có: đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên \(a \bot AB;a \bot CD\).
Suy ra: AB // CD.
b) Đường thẳng a là đường trung trực của đoạn thẳng AB và CD nên MN là đường trung trực của đoạn thẳng AB và CD. Suy ra: MD = MC.
Xét tam giác vuông MNC và tam giác vuông MND có: ND = NC; MD = MC.
Vậy \(\Delta MNC = \Delta MND\)(cạnh huyền – cạnh góc vuông).
c) \(\Delta MNC = \Delta MND\)nên \(\widehat {CMN} = \widehat {DMN}\).
Mà \(\widehat {AMN} = \widehat {BMN} = 90^\circ \Rightarrow \widehat {AMN} – \widehat {DMN} = \widehat {BMN} – \widehat {CMN}\).
Vậy \(\widehat {AMD} = \widehat {BMC}\).
d) Xét hai tam giác AMD và BMC có:
MA = MB;
\(\widehat {AMD} = \widehat {BMC}\);
MD = MC.
Vậy \(\Delta MAD = \Delta MBC\)(c.g.c). Suy ra: \(AD = BC,\widehat A = \widehat B\) (cặp cạnh và góc tương ứng).
e) \(\Delta MAD = \Delta MBC\) nên \(\widehat {ADM} = \widehat {BCM}\) (2 góc tương ứng).
\(\Delta MNC = \Delta MND\) nên \(\widehat {MCN} = \widehat {MDN}\) (2 góc tương ứng).
Vậy \(\widehat {ADM} + \widehat {MDN} = \widehat {BCM} + \widehat {MCN}\) hay \(\widehat {ADC} = \widehat {BCD}\).