Chứng minh \(\widehat {CAD} = \widehat {CBD}\) bằng cách chứng minh \(\widehat {CAB} – \widehat {DAB} = \widehat {CBA} – \widehat {DBA}\). Hướng dẫn trả lời Giải bài 1 trang 103 SGK Toán 7 tập 2 – Cánh diều – Bài 9. Đường trung trực của một đoạn thẳng. Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB….
Đề bài/câu hỏi:
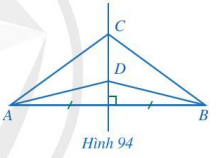
Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh \(\widehat {CAD} = \widehat {CBD}\).
Hướng dẫn:
Chứng minh \(\widehat {CAD} = \widehat {CBD}\) bằng cách chứng minh \(\widehat {CAB} – \widehat {DAB} = \widehat {CBA} – \widehat {DBA}\).
Lời giải:
Ta có: đường thẳng CD là đường trung trực của đoạn thẳng AB nên CA=CB và DA=DB.
Ta có tam giác ABC cân tại C, tam giác DAB cân tại D
Suy ra \(\widehat {CAB} = \widehat {CBA};\widehat {DAB} = \widehat {DBA}\).
Vậy \(\widehat {CAB} – \widehat {DAB} = \widehat {CBA} – \widehat {DBA}\) suy ra: \(\widehat {CAD} = \widehat {CBD}\).