Giải chi tiết Lời giải Đề thi giữa kì 2 – Đề số 4 – Đề thi đề kiểm tra Toán lớp 7 Cánh diều.
Câu hỏi/Đề bài:
I. Trắc nghiệm
|
1.B |
2. D |
3. A |
4. C |
|
5. A |
6. D |
7. D |
8. C |
Câu 1.
Hướng dẫn:
Đọc và miêu tả dữ liệu từ bảng thống kê.
Cách giải:
Loại nước ít người ưa chuộng nhất là nước dứa.
Chọn B.
Câu 2.
Phương pháp:
Dùng các chữ, các số và các phép toán để diễn đạt các mệnh đề phát biểu bằng lời.
Cách giải:
Bình phương của một tổng hai số \(a\) và \(b\) là: \({\left( {a + b} \right)^2}\)
Chọn D.
Câu 3.
Hướng dẫn:
Thay \(x = – 2\) vào biểu thức \({x^3} – 2{x^2}\) để tính.
Cách giải:
Thay \(x = – 2\) vào biểu thức \({x^3} – 2{x^2}\) ta có: \({\left( { – 2} \right)^3} – 2.{\left( { – 2} \right)^2} = \left( { – 8} \right) – 2.4 = – 16\)
Chọn A.
Câu 4.
Hướng dẫn:
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
Cách giải:
Biểu thức: \(2xy – {x^2}\) không là một đơn thức.
Chọn C.
Câu 5.
Hướng dẫn:
Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
Cách giải:
Sắp xếp theo lũy thừa giảm dần của biến: \(P\left( x \right) = {x^4} + 2{x^3} – 7{x^2} – 4\)
Chọn A.
Câu 6.
Hướng dẫn:
Sử dụng hệ quả của bất đẳng thức trong tam giác:
+ Tồn tại một tam giác có độ dài ba cạnh là \(a,b,c\) nếu \(\left| {b – c} \right| < a < b + c\).
+ Trong trường hợp xác định được \(a\) là số lớn nhất trong ba số \(a,b,c\) thì điều kiện tồn tại tam giác là \(a < b + c\).
Cách giải:
Xét tam giác \(MNP\), ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\left| {NP – MP} \right| < MN < NP + MP\\ \Rightarrow \left| {1 – 7} \right| < MN < 1 + 7\\ \Rightarrow 6 < MN < 8\end{array}\)
Vì độ dài cạnh \(MN\) là một số nguyên nên \(MN = 7\,\left( {cm} \right)\)
Chọn D.
Câu 7.
Hướng dẫn:
Sử dụng quan hệ giữa góc và cạnh đối diện trong tam giác.
Cách giải:
Xét \(\Delta ABC\) có: \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác)
\(\begin{array}{l} \Rightarrow {90^0} + \angle B + {30^0} = {180^0}\\ \Rightarrow \angle B + {120^0} = {180^0}\\ \Rightarrow \angle B = {60^0}\end{array}\)
Ta có: \(\angle C < \angle B < \angle A\) (vì \({30^0} < {60^0} < {90^0}\))
\( \Rightarrow AB < AC < BC\) (quan hệ giữa góc và cạnh đối diện trong tam giác)
Chọn D.
Câu 8.
Hướng dẫn:
Tính chất đồng quy của 3 đường trung trực của tam giác
Lời giải
3 đường trung trực của tam giác đồng quy tại 1 điểm, điểm này cách đều 3 đỉnh của tam giác.
Chọn C.
II. PHẦN TỰ LUẬN (8,0 điểm)
Bài 1.
Hướng dẫn:
a) Đọc và mô tả biểu đồ hình quạt tròn.
b) Thực hiện phép chia.
c) Số lao động có trình độ đại học trở lên năm 2020 = % tương ứng . số người lao động.
Cách giải:
a) Trong năm 2020, có:
+ 76% lực lượng lao động không có trình độ CMKT;
+ 4,7% lực lượng lao động có trình độ sơ cấp;
+ 4,4 % lực lượng lao động có trình độ trung cấp;
+ 3,8% lực lượng lao động có trình độ cao đẳng;
+ 11,1% lực lượng lao động có trình độ đại học trở lên.
b) Từ biểu đồ hình quạt tròn, ta thấy 76% lực lượng lao động không có trình độ CMKT; 11,1% lực lượng lao động có trình độ đại học trở lên.
Ta có: \(76\% :11,1\% = \dfrac{{76}}{{100}}:\dfrac{{11,1}}{{100}} = \dfrac{{76}}{{100}}.\dfrac{{100}}{{11,1}} = \dfrac{{76}}{{11,1}} = 6,\left( {846} \right) \approx 7\)
Vậy lực lượng lao động không có trình độ CMKT gấp 7 lần lực lượng lao động có trình độ đại học trở lên.
c) Số lao động có trình độ đại học trở lên năm 2020 là: \(11,1\% .54,6 = \dfrac{{11,1}}{{100}}.\dfrac{{546}}{{10}} = 6,0606 \approx 6,06\) (triệu người)
Bài 2.
Hướng dẫn:
a) Thu gọn đa thức bằng cách nhóm các hạng tử đồng dạng lại rồi thu gọn chúng. Sau đó sắp xếp theo lũy thừa giảm dần của biến.
b) Tính \(f\left( x \right) + g\left( x \right)\) ta nhóm các hạng tử đồng dạng lại rồi thu gọn chúng.
Tìm nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\), ta giải phương trình \(f\left( x \right) + g\left( x \right) = 0\)
Cách giải:
a) \(f\left( x \right) = {x^5} + {x^3} – 4x – {x^5} + 3x + 7\)
\(\begin{array}{l}f\left( x \right) = \left( {{x^5} – {x^5}} \right) + {x^3} + \left( { – 4x + 3x} \right) + 7\\f\left( x \right) = {x^3} – x + 7\end{array}\)
\(\begin{array}{l}g\left( x \right) = 3{x^2} – {x^3} + 8x – 3{x^2} – 14\\g\left( x \right) = – {x^3} + \left( {3{x^2} – 3{x^2}} \right) + 8x – 14\\g\left( x \right) = – {x^3} + 8x – 14\end{array}\)
b) \(f\left( x \right) + g\left( x \right) = {x^3} – x + 7 – {x^3} + 8x – 14\)
\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {x^3} – x + 7 – {x^3} + 8x – 14\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{x^3} – {x^3}} \right) + \left( { – x + 8x} \right) + \left( {7 – 14} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 7x – 7\end{array}\)
Ta có: \(f\left( x \right) + g\left( x \right) = 0\)
\(\begin{array}{l}7x – 7 = 0\\7x = 7\\\,\,\,x = 1\end{array}\)
Vậy \(x = 1\) là nghiệm của đa thức \(f\left( x \right) + g\left( x \right)\)
Bài 3.
Hướng dẫn:
+ Sử dụng các cách chứng minh hai tam giác bằng nhau.
+ Mối quan hệ giữa góc và cạnh trong tam giác (Cạnh đối diện với góc lớn hơn thì lớn hơn)
+ Tính chất trọng tâm của tam giác.
Cách giải:
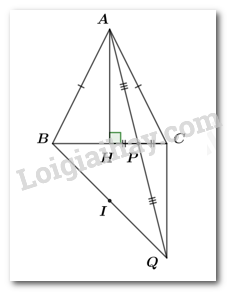
a. Xét \(\Delta APH\)và \(\Delta QPC\)có:
+ \(HP = PC\)(gt)
+ \(\angle APH = \angle QPC\)(đối đỉnh)
+ \(QP = PA\) (gt)
\( \Rightarrow \)\(\Delta APH = \Delta QPC\) (c.g.c) (đpcm).
\( \Rightarrow \angle AHP = \angle QCP = {90^o}\)(hai góc tương ứng)
\( \Rightarrow QC \bot BC\)(đpcm).
b. Theo (a) \(\Delta APH = \Delta QPC\)
\( \Rightarrow QC = AH\)(hai cạnh tương ứng) (1)
Mà \(\Delta AHC\)vuông tại H \( \Rightarrow AH < AC\)(cạnh góc vuông <cạnh huyền) (2)
Từ (1) và (2), suy ra \(QC < AC\)(đpcm).
c. Xét \(\Delta AQC\)có \(QC < AC\)\( \Rightarrow \angle QAC < \angle AQC\) (3) (Mối quan hệ giữa cạnh- góc trong tam giác)
Mặt khác \(\Delta APH = \Delta QPC \Rightarrow \angle HAP = \angle PQC = \angle AQC\) (4)
Từ (3) và (4) \( \Rightarrow \angle HAP < \angle QAC\) hay \(\angle HAP < \angle PAC\)(đpcm).
d. Xét \(\Delta ABQ\)có \(BP\)là trung tuyến ứng với cạnh \(AQ\)
Mà \(BH = 2HP\)(do \(H\) là trung điểm của \(BC\), \(P\)là trung điểm của \(HC\)) \( \Rightarrow H\)là trọng tâm \(\Delta ABQ\) (5)
Lại có \(I\)là trung điểm của \(BQ\) \( \Rightarrow AI\)là trung tuyến ứng với cạnh \(BQ\) (6)
Từ (5), (6) \( \Rightarrow H \in AI\)
\( \Rightarrow A,H,I\)thẳng hàng (đpcm)
Bài 4.
Hướng dẫn:
Áp dụng tính chất của dãy tỉ số bằng nhau.
Cách giải:
Ta có: \(\dfrac{a}{b} = \dfrac{b}{c} = \dfrac{c}{d} = \dfrac{d}{e}\) nên \(\dfrac{a}{b} = \dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: \(\dfrac{{2019b}}{{2019c}} = \dfrac{{2020c}}{{2020d}} = \dfrac{{2021d}}{{2021e}} = \dfrac{{2019b + 2020c – 2021d}}{{2019c + 2020d – 2021e}}\)
Mà \(\dfrac{a}{b} = \dfrac{{2019b}}{{2020c}}\) và \(\dfrac{a}{b} = \dfrac{b}{c}\) (gt) nên \({\left( {\dfrac{{2019b + 2020c – 2021d}}{{2019c + 2020d – 2021e}}} \right)^3} = {\left( {\dfrac{a}{b}} \right)^3} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{a}{b} = \dfrac{{{a^2}}}{{{b^2}}}.\dfrac{b}{c} = \dfrac{{{a^2}}}{{bc}}\) (đpcm)