Đáp án Câu hỏi Vận dụng 2 trang 12 SGK Toán 12 Kết nối tri thức – Bài 1. Tính đơn điệu và cực trị của hàm số. Tham khảo: Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\.
Câu hỏi/Đề bài:
Một vật được phóng thẳng đứng lên trên từ độ cao 2m với vận tốc ban đầu là 24,5m/s. Trong Vật lí, ta biết rằng khi bỏ qua sức cản của không khí thì độ cao h (mét) của vật sau t (giây) được cho bởi công thức: \(h\left( t \right) = 2 + 24,5t – 4,9{t^2}\). Hỏi tại thời điểm nào thì vật đạt độ cao lớn nhất?
Hướng dẫn:
Sử dụng kiến thức về cách tìm cực trị của hàm số \(y = f\left( x \right)\) để tìm thời điểm vật đạt độ cao lớn nhất:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm f’(x). Tìm các điểm mà tại đó đạo hàm f’(x) bằng 0 hoặc đạo hàm không tồn tại.
3. Lập bảng biến thiên của hàm số.
4. Từ bảng biến thiên suy ra các cực trị của hàm số.
Lời giải:
Xét hàm số: \(h\left( t \right) = 2 + 24,5t – 4,9{t^2}\).
Tập xác định của hàm số là \(\mathbb{R}\).
Ta có: \[h’\left( t \right) = – 9,8t + 24,5;h’\left( t \right) = 0 \Leftrightarrow – 9,8t + 24,5 = 0 \Leftrightarrow t = \frac{5}{2}\].
Bảng biến thiên:
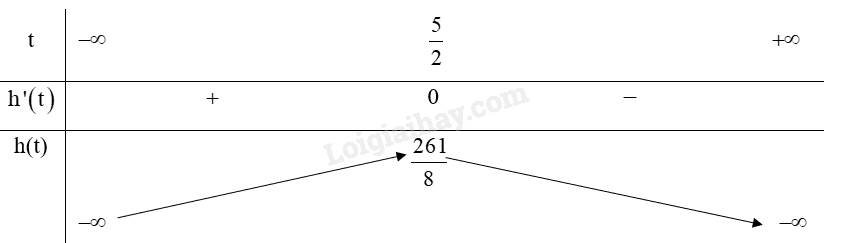
Từ bảng biến thiên ta có:
Hàm số đạt cực đại tại \(t = \frac{5}{2}\),
Vậy thời điểm vật đạt độ cao lớn nhất là \(t = \frac{5}{2}\) giây