Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến của hàm số. Hướng dẫn giải Giải bài tập 1.1 trang 13 SGK Toán 12 tập 1 – Kết nối tri thức – Bài 1. Tính đơn điệu và cực trị của hàm số. Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:…
Đề bài/câu hỏi:
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
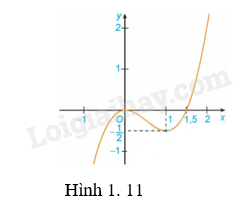
a) Đồ thị hàm số \(y = {x^3} – \frac{3}{2}{x^2}\) (H.1.11);
Tìm các khoảng đồng biến, khoảng nghịch biến của các hàm số có đồ thị như sau:
a) Đồ thị hàm số \(y = {x^3} – \frac{3}{2}{x^2}\) (H.1.11);
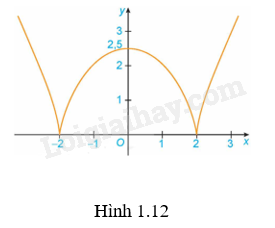
b) Đồ thị hàm số \(y = \sqrt[3]{{{{\left( {{x^2} – 4} \right)}^2}}}\) (H.1.12).
Hướng dẫn:
Sử dụng kiến thức về tính đồng biến, nghịch biến của hàm số để tìm khoảng đồng biến, nghịch biến của hàm số:
+ Nếu hàm số đồng biến trên K thì đồ thị của hàm số đi lên từ trái sang phải.
+ Nếu hàm số nghịch biến trên K thì đồ thị của hàm số đi xuống từ trái sang phải.
Lời giải:
a) Hàm số \(y = {x^3} – \frac{3}{2}{x^2}\) đồng biến trên \(\left( { – \infty ;0} \right)\) và \(\left( {1; + \infty } \right)\).
Hàm số \(y = {x^3} – \frac{3}{2}{x^2}\) nghịch biến trên \(\left( {0;1} \right)\).
b) Hàm số \(y = \sqrt[3]{{{{\left( {{x^2} – 4} \right)}^2}}}\) đồng biến trên \(\left( { – 2;0} \right)\) và \(\left( {2; + \infty } \right)\).
Hàm số \(y = \sqrt[3]{{{{\left( {{x^2} – 4} \right)}^2}}}\) nghịch biến trên \(\left( { – \infty ; – 2} \right)\) và \(\left( {0;2} \right)\).