Sử dụng kiến thức về tọa độ trung điểm của đoạn thẳng để tính: Trong không gian Oxyz, cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\. Hướng dẫn trả lời Giải bài tập 2.23 trang 72 SGK Toán 12 tập 1 – Kết nối tri thức – Bài 8. Biểu thức tọa độ của các phép toán vectơ. Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m,…
Đề bài/câu hỏi:
Một phòng học có thiết kế dạng hình hộp chữ nhật với chiều dài là 8m, chiều rộng là 6m và chiều cao là 3m. Một chiếc đèn được treo tại chính giữa trần nhà của phòng học. Xét hệ trục tọa độ Oxyz có gốc O trùng với một góc phòng và mặt phẳng (Oxy) trùng với mặt sàn, đơn vị đo được lấy theo mét (H.2.51). Hãy tìm tọa độ của điểm treo đèn.
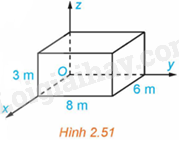
Hướng dẫn:
Sử dụng kiến thức về tọa độ trung điểm của đoạn thẳng để tính: Trong không gian Oxyz, cho hai điểm \(A\left( {{x_A};{y_A};{z_A}} \right)\) và \(B\left( {{x_B};{y_B};{z_B}} \right)\). Khi đó, tọa độ trung điểm của đoạn thẳng AB là: \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\).
Lời giải:
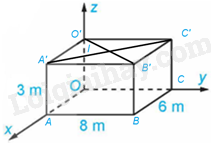
Đặt tên các điểm như hình vẽ.
Khi đó, \(O’\left( {0;0;3} \right),B’\left( {8;6;3} \right)\).
Vì phòng học thiết kế dạng hình hộp chữ nhật nên hình O’C’B’A’ là hình chữ nhật. Gọi là giao điểm của hai đường chéo O’B’ và A’C’ nên I là trung điểm của O’B’.
Vì đèn được treo tại chính giữa trần nhà của phòng học nên đèn trùng với I.
Do đó: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_{O’}} + {x_{B’}}}}{2} = 4\\{y_I} = \frac{{{y_{O’}} + {y_{B’}}}}{2} = 3\\{z_I} = \frac{{{z_{O’}} + {z_{B’}}}}{2} = 3\end{array} \right.\). Suy ra, I(4; 3; 3). Vậy tọa độ của điểm treo đèn là (4; 3; 3).