Giải Câu hỏi Vận dụng 2 trang 27 SGK Toán 12 Chân trời sáng tạo – Bài 3. Ứng dụng hình học của tích phân.
Câu hỏi/Đề bài:
Sử dụng tích phân, tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\). (hình 16)
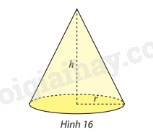
Hướng dẫn:
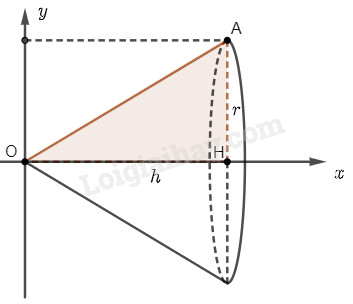
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Thể tích của khối nón là \(V = \pi \int\limits_0^h {{f^2}\left( x \right)dx} \)
Lời giải:
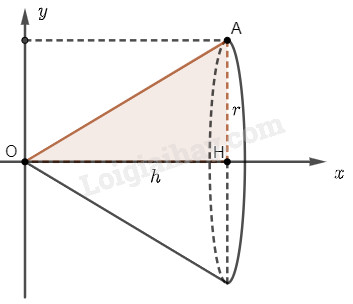
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Đường thẳng \(OA\) đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {h;r} \right)\) nên phương trình đường thẳng \(OA\) là \(y = \frac{r}{h}x\).
Thể tích khối nón là:
\(V = \pi \int\limits_0^h {{{\left( {\frac{r}{h}x} \right)}^2}dx} = \pi \frac{{{r^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{\pi {r^2}}}{{{h^2}}}.\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{\pi {r^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{\pi {r^2}h}}{3}\)