Đáp án Câu hỏi Thực hành 6 trang 26 SGK Toán 12 Chân trời sáng tạo – Bài 3. Ứng dụng hình học của tích phân. Hướng dẫn: Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\), với \(D\.
Câu hỏi/Đề bài:
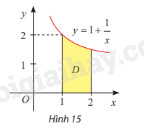
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 1 + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) (hình 15). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Hướng dẫn:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\), với \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\), là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Lời giải:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_1^2 {{{\left( {1 + \frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {\left( {1 + \frac{2}{x} + \frac{1}{{{x^2}}}} \right)dx} = \pi \left. {\left( {x + 2\ln \left| x \right| – \frac{1}{x}} \right)} \right|_1^2 = \pi \left( {\frac{3}{2} + 2\ln 2} \right)\)