Trả lời Câu hỏi Thực hành 9 trang 50 SGK Toán 12 Chân trời sáng tạo – Bài 1. Vectơ và các phép toán trong không gian. Gợi ý: Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u . \overrightarrow v = |\overrightarrow u |.
Câu hỏi/Đề bài:
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1.
a) Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {A’C’} \), \(\overrightarrow {AB} .\overrightarrow {CC’} \)
b) Tính góc \((\overrightarrow {AC} .\overrightarrow {AC’} )\) (kết quả làm tròn đến phút)
Hướng dẫn:
a) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
b) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Lời giải:
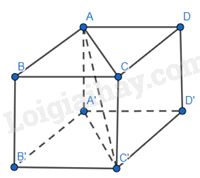
a) \(\overrightarrow {AB} .\overrightarrow {A’C’} = \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = 1.\sqrt 2 .\cos 45^\circ = \frac{1}{2}\)
\(\overrightarrow {AB} .\overrightarrow {CC’} = \overrightarrow {AB} .\overrightarrow {BB’} = 0\) vì \(\overrightarrow {AB} \bot \overrightarrow {BB’} \)
b) Xét tam giác CAC’ vuông tại C:
\(AC = \sqrt 2 \); CC’ = 1 => \(\tan (\overrightarrow {AC} ,\overrightarrow {AC’} ) = \tan \widehat {C’AC} = \frac{{CC’}}{{AC}} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {C’AC} = 45^\circ \)