Hướng dẫn giải Câu hỏi Khám phá 6 trang 49 SGK Toán 12 Chân trời sáng tạo – Bài 1. Vectơ và các phép toán trong không gian. Gợi ý: Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không.
Câu hỏi/Đề bài:
Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) thoả mãn \(|\overrightarrow u | = 2\) , \(|\overrightarrow v | = 3\). Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \), \(\overrightarrow {AC} = \overrightarrow v \) (Hình 24). Giả sử \(\widehat {BAC} = 60^\circ \)
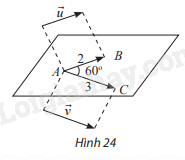
a) Tính góc \((\overrightarrow u ,\overrightarrow v )\)
b) Trong mặt phẳng (ABC), tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \)
Hướng dẫn:
a) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
Lời giải:
a) Góc \((\overrightarrow u ,\overrightarrow v )\) = \(\widehat {BAC} = 60^\circ \)
b) \(\overrightarrow {AB} .\overrightarrow {AC} \) = \(AB.AC.\cos \widehat {BAC} = 2.3.\cos 60^\circ = 3\)