Giải chi tiết Câu hỏi Khám phá 2 trang 23 SGK Toán 12 Chân trời sáng tạo – Bài 3. Ứng dụng hình học của tích phân. Hướng dẫn: Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\).
Câu hỏi/Đề bài:
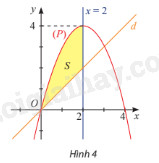
Cho hai hàm số \(y = 4x – {x^2}\) và \(y = x\) lần lượt có đồ thị \(\left( P \right)\) và \(d\) như hình 4.
a) Tính diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\).
b) Tính diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\).
Hướng dẫn:
a) Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x – {x^2}} \right|dx} \)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Suy ra diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} – {S_2}\).
Lời giải:
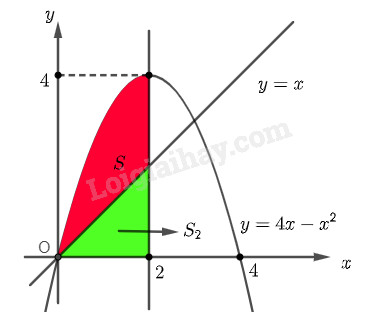
Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x – {x^2}} \right|dx} \)
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(4x – {x^2} \ge 0\), do đó:
\({S_1} = \int\limits_0^2 {\left( {4x – {x^2}} \right)dx} = \left. {\left( {2{x^2} – \frac{{{x^3}}}{3}} \right)} \right|_0^2 = \frac{{16}}{3}\)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(x \ge 0\), do đó:
\({S_2} = \int\limits_0^2 {xdx} = \left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^2 = 2\)
Vậy diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} – {S_2} = \frac{{16}}{3} – 2 = \frac{{10}}{3}\).