Giải chi tiết Câu hỏi Hoạt động 2 trang 44 SGK Toán 12 Chân trời sáng tạo – Giải mục 1 trang 44 – 45 – 46 – 47 SGK Toán 12 tập 2. Tham khảo: Chỉ ra rằng \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương.
Câu hỏi/Đề bài:
Trong không gian \(Oxyz\), cho đường thẳng \(d\) đi qua điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) cố định và có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) khác \(\vec 0.\)
a) Giải thích tại sao ta có thể viết \(M \in d \Leftrightarrow \overrightarrow {{M_0}M} = t\vec a{\rm{ }}\left( {t \in \mathbb{R}} \right).\)
b) Với \(M\left( {x;y;z} \right)\) thuộc \(d\), hãy tính \(x\), \(y\), \(z\) theo \({x_0}\), \({y_0}\), \({z_0}\) và \({a_1}\), \({a_2}\), \({a_3}.\)
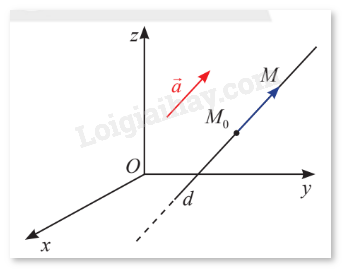
Hướng dẫn:
a) Chỉ ra rằng \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương.
b) Sử dụng tính chất của hai vectơ cùng phương.
Lời giải:
a) Ta có \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\).
Nếu \(M \in d\), ta có \(d\) đi qua hai điểm \(M\) và \({M_0}\) nên hai vectơ \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương, suy ra \(\overrightarrow {{M_0}M} = t\vec a\) với \(t \in \mathbb{R}\).
Ngược lại, với \(\overrightarrow {{M_0}M} = t\vec a\) thì \(\overrightarrow {{M_0}M} \) và \(\vec a\) là hai vectơ cùng phương. Mà \(\vec a\) là vectơ chỉ phương của đường thẳng \(d\), nên \(\overrightarrow {{M_0}M} \) cũng là một vectơ chỉ phương của đường thẳng \(d\). Do \({M_0} \in d\), nên ta suy ra \(M \in d\).
b) Ta có \(\overrightarrow {{M_0}M} = \left( {x – {x_0};y – {y_0};z – {z_0}} \right)\) và \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\).
Theo câu a, ta có \(\overrightarrow {{M_0}M} = t\vec a\) nên \(\left( {x – {x_0};y – {y_0};z – {z_0}} \right) = t\left( {{a_1};{a_2};{a_3}} \right)\)
Suy ra \(\left\{ \begin{array}{l}x – {x_0} = t{a_1}\\y – {y_0} = t{a_2}\\z – {z_0} = t{a_3}\end{array} \right.\) hay \(\left\{ \begin{array}{l}x = {x_0} + t{a_1}\\y = {y_0} + t{a_2}\\z = {z_0} + t{a_3}\end{array} \right.\)