Câu hỏi Luyện tập 3 trang 7 Toán 12 Cánh diều: Chứng minh rằng hàm số y = √x^2 + 1 nghịch biến trên nửa khoảng ( – ∇ ;0] và đồng biến trên nửa khoảng [0

Câu hỏi/Đề bài:

Chứng minh rằng hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( – \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).

Hướng dẫn:

B1: Tìm tập xác định của hàm số.

B2: Tính \(y’\). Tìm các điểm mà tại đó \(y’ = 0\) hoặc \(y’\) không tồn tại.

B3: Lập bảng biến thiên của hàm số.

B4: Dựa vào bảng biến thiên để kết luận.

Lời giải:

Tập xác định \(D = \mathbb{R}\).

Ta có: \(y’ = \frac{x}{{\sqrt {{x^2} + 1} }}\).

Xét \(y’ = 0 \Leftrightarrow x = 0\).

Ta có bảng biến thiên:

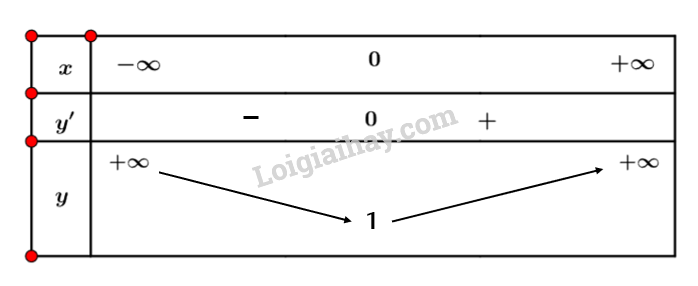
Vậy hàm số \(y = \sqrt {{x^2} + 1} \) nghịch biến trên nửa khoảng \(( – \infty ;0]\) và đồng biến trên nửa khoảng \([0; + \infty )\).