Hướng dẫn giải Giải bài 2.21 trang 49 sách bài tập toán 12 – Kết nối tri thức – Bài 7. Hệ trục tọa độ trong không gian. Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao bằng 5 và độ dài cạnh đáy bằng 4….
Đề bài/câu hỏi:
Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao bằng 5 và độ dài cạnh đáy bằng 4. Hãy xác định tọa độ các điểm \(S,A,B,C,D\) đối với hệ tọa độ \(Oxyz\) có gốc \(O\) trùng với tâm của hình vuông \(ABCD\), tia \(Ox\) chứa \(B\), tia \(Oy\) chứa \(C\) và tia \(Oz\) chứa \(S\).
Lập hệ trục tọa độ theo giả thiết và xác định tọa độ từng điểm.
Hướng dẫn:
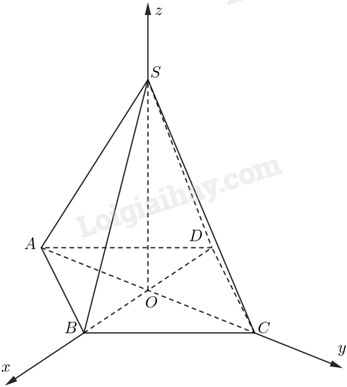
Lời giải:
Ta có \(S\) thuộc tia \(Oz\) và \(OS = 5\) nên \(S\left( {0;0;5} \right)\).
Do \(ABCD\) là hình vuông cạnh \(4\) nên \(OA = OB = OC = OD = 2\sqrt 2 \).
Ta có \(B\) thuộc tia \(Ox\) và \(OB = 2\sqrt 2 \) suy ra \(B\left( {2\sqrt 2 ;0;0} \right)\); \(D\) thuộc tia đối của tia \(Ox\) và \(OD = 2\sqrt 2 \) suy ra \(D\left( { – 2\sqrt 2 ;0;0} \right)\).
Tương tự có \(C\) thuộc tia \(Oy\) và \(OC = 2\sqrt 2 \) suy ra \(C\left( {0;2\sqrt 2 ;0} \right)\); \(A\) thuộc tia đối của tia \(Oy\) và \(OA = 2\sqrt 2 \) suy ra \(A\left( {0; – 2\sqrt 2 ;0} \right)\).
Vậy \(S\left( {0;0;5} \right)\), \(A\left( {0; – 2\sqrt 2 ;0} \right)\), \(B\left( {2\sqrt 2 ;0;0} \right)\), \(C\left( {0;2\sqrt 2 ;0} \right)\) và \(D\left( { – 2\sqrt 2 ;0;0} \right)\).