Xét hàm số \(y = f\left( x \right)\), lập bảng biến thiên. Hướng dẫn cách giải/trả lời Giải bài 8 trang 11 sách bài tập toán 12 – Chân trời sáng tạo – Bài 1. Tính đơn điệu và cực trị của hàm số. Chứng minh rằng: a) Phương trình \({x^3} + 5{x^2} – 8{\rm{x}} + 4 = 0\) có duy nhất một nghiệm….
Đề bài/câu hỏi:
Chứng minh rằng:
a) Phương trình \({x^3} + 5{x^2} – 8{\rm{x}} + 4 = 0\) có duy nhất một nghiệm.
b) Phương trình \( – {x^3} + 3{x^2} + 24x – 1 = 0\) có ba nghiệm phân biệt.
Hướng dẫn:
Xét hàm số \(y = f\left( x \right)\), lập bảng biến thiên, xem xét giao điểm của đồ thị hàm số với đường thẳng \(y = 0\) và kết luận.
Lời giải:
a) Đặt \(y = {x^3} + 5{x^2} – 8{\rm{x}} + 4\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y’ = 3{x^2} + 10x – 8;y’ = 0 \Leftrightarrow x = – 4\) hoặc \({\rm{x}} = \frac{2}{3}\).
Bảng biến thiên:
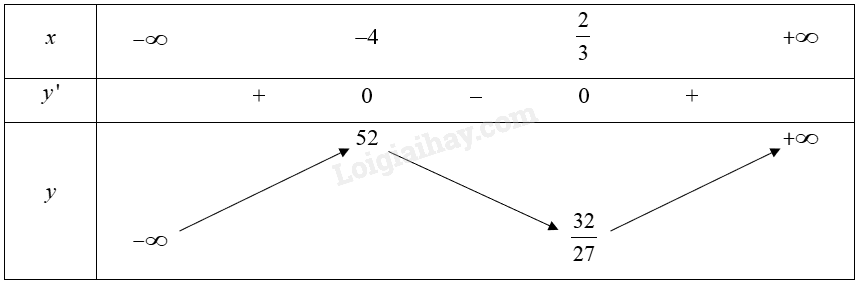
Từ bảng biển thiên, ta thấy đường thẳng \(y = 0\) giao với đồ thị của hàm số tại đúng một điểm trong khoảng \(\left( { – \infty ; – 4} \right)\). Do đó phương trình \({x^3} + 5{x^2} – 8{\rm{x}} + 4 = 0\) có duy nhất một nghiệm.
b) Đặt \(y = – {x^3} + 3{x^2} + 24x – 1\).
Tập xác định: \(D = \mathbb{R}\).
Ta có \(y’ = – 3{x^2} + 6x + 24;y’ = 0 \Leftrightarrow x = 4\) hoặc \({\rm{x}} = – 2\).
Bảng biến thiên:
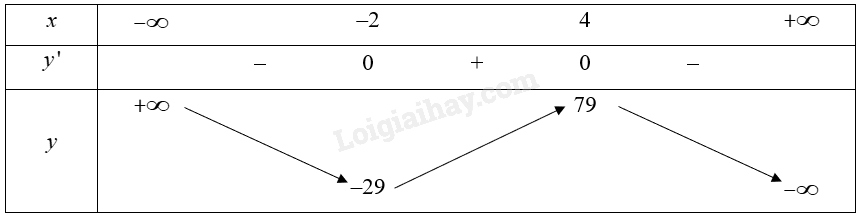
Từ bảng biển thiên, ta thấy đường thẳng \(y = 0\) giao với đồ thị của hàm số tại ba điểm phân biệt. Do đó phương trình \( – {x^3} + 3{x^2} + 24x – 1 = 0\) có ba nghiệm phân biệt.