Xét hàm số \(y = \frac{{{x^2} + x + 4}}{{x + 1}}\), lập bảng biến thiên. Hướng dẫn trả lời Giải bài 9 trang 11 sách bài tập toán 12 – Chân trời sáng tạo – Bài 1. Tính đơn điệu và cực trị của hàm số. Tìm \(m\) để phương trình \(\frac{{{x^2} + x + 4}}{{x + 1}} = m\) có hai nghiệm phân biệt….
Đề bài/câu hỏi:
Tìm \(m\) để phương trình \(\frac{{{x^2} + x + 4}}{{x + 1}} = m\) có hai nghiệm phân biệt.
Hướng dẫn:
Xét hàm số \(y = \frac{{{x^2} + x + 4}}{{x + 1}}\), lập bảng biến thiên, xét sự tương giao của đồ thị hàm số với đường thẳng \(y = m\) và kết luận.
Lời giải:
Đặt \(y = \frac{{{x^2} + x + 4}}{{x + 1}}\).
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { – 1} \right\}\).
Ta có
\(y’ = \frac{{{{\left( {{x^2} + x + 4} \right)}^\prime }\left( {x + 1} \right) – \left( {{x^2} + x + 4} \right){{\left( {x + 1} \right)}^\prime }}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{\left( {2{\rm{x}} + 1} \right)\left( {x + 1} \right) – \left( {{x^2} + x + 4} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2{\rm{x}} – 3}}{{{{\left( {x + 1} \right)}^2}}}\)
\(y’ = 0 \Leftrightarrow x = 1\) hoặc \({\rm{x}} = – 3\).
Bảng biến thiên:
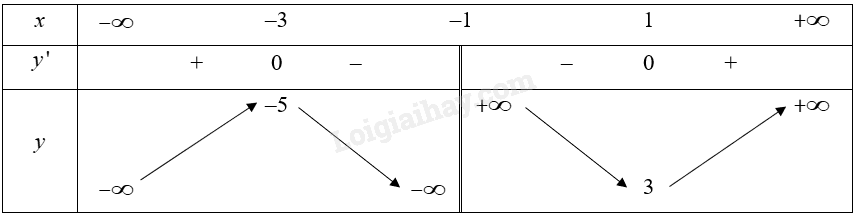
Từ bảng biển thiên, ta thấy đường thẳng \(y = m\) giao với đồ thị của hàm số tại hai nghiệm phân biệt khi \(m > 3\) hoặc \(m 3\) hoặc \(m < – 5\).