Từ đồ thị hàm số \(y = f’\left( x \right)\), lập bảng biến thiên của hàm số \(y = f\left( x \right)\. Trả lời Giải bài 6 trang 11 sách bài tập toán 12 – Chân trời sáng tạo – Bài 1. Tính đơn điệu và cực trị của hàm số. Đạo hàm (f’left( x right)) của hàm số (y = fleft( x right)) có đồ thị như Hình 4….
Đề bài/câu hỏi:
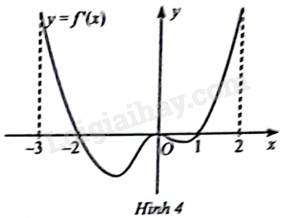
Đạo hàm \(f’\left( x \right)\) của hàm số \(y = f\left( x \right)\) có đồ thị như Hình 4. Xét tính đơn điệu và tìm các điểm cực trị của hàm số \(y = f\left( x \right)\).
Hướng dẫn:
Từ đồ thị hàm số \(y = f’\left( x \right)\), lập bảng biến thiên của hàm số \(y = f\left( x \right)\) rồi xác định tính đồng biến, nghịch biến, cực trị của hàm số.
Lời giải:
Từ đồ thị, ta có \(f’\left( x \right) > 0\) trên các khoảng \(\left( { – 3; – 2} \right)\) và \(\left( {1;2} \right)\), \(f’\left( x \right) < 0\) trên các khoảng \(\left( { – 2;0} \right)\) và \(\left( {0;1} \right)\). Do đó ta có bảng biến thiên:

Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng \(\left( { – 3; – 2} \right)\) và \(\left( {1;2} \right)\), nghịch biến trên khoảng \(\left( { – 2;1} \right)\).
Hàm số đạt cực đại tại \(x = – 2\) và đạt cực tiểu tại \({\rm{x}} = 1\).