‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A};{z_B} – {z_A}} \right)\). Phân tích, đưa ra lời giải Giải bài 17 trang 67 sách bài tập toán 12 – Cánh diều – Bài 2. Tọa độ của vecto. Trong quá trình cất cánh của một máy bay không người lái: Ban đầu máy bay ở vị trí \(A\),…
Đề bài/câu hỏi:
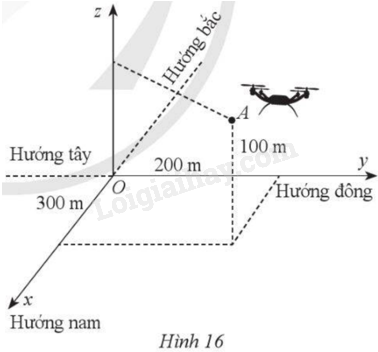
Trong quá trình cất cánh của một máy bay không người lái: Ban đầu máy bay ở vị trí \(A\), máy bay cách vị trí điều khiển 300 m về phía nam và 200 m về phía đông, đồng thời cách mặt đất 100 m (Hình 16). Một phút sau, máy bay ở vị trí \(B\) cách vị trí điều khiển 1 200 m về phía nam và 2 100 m về phía đông, đồng thời cách mặt đất 250 m.
Chọn hệ trục toạ độ \(Oxyz\) với gốc \(O\) trùng với vị trí điều khiển, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất, trục \(Ox\) có hướng trùng với hướng nam, trục \(Oy\) có hướng trùng với hướng đông, trục \(Oz\) vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên trục tương ứng với 1 m. Hãy xác định toạ độ vectơ dịch chuyển \(\overrightarrow {AB} \) của máy bay không người lái đó.
Hướng dẫn:
‒ Sử dụng toạ độ của vectơ \(\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A};{z_B} – {z_A}} \right)\).
Lời giải:
Từ giả thiết ta có toạ độ của điểm \(A\left( {300;200;100} \right)\), toạ độ của điểm \(B\left( {1200;2100;250} \right)\).
Do đó, ta có: \(\overrightarrow {AB} = \left( {1200 – 300;2100 – 200;250 – 100} \right) = \left( {900;1900;150} \right)\).