Hướng dẫn giải Hoạt động 1 Bài 3. Hàm số lượng giác và đồ thị (trang 22, 23, 24) – SGK Toán 11 Cánh diều. Hướng dẫn: Dựa vào kiến thức về hàm số để xác định.
Câu hỏi/Đề bài:
a) Cho hàm số \(f\left( x \right) = {x^2}\)
Với \(x \in \mathbb{R}\), hãy so sánh \(f\left( { – x} \right)\) và \(f\left( x \right)\)
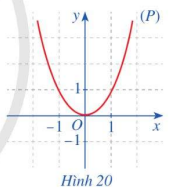
Quan sát parabol (P) là đồ thị của hàm số \(f\left( x \right) = {x^2}\) (Hình 20) và cho biết trục đối xứng của (P) là đường thẳng nào?
b) Cho hàm số \(g\left( x \right) = x\)
Với \(x \in \mathbb{R}\), hãy so sánh \(g\left( { – x} \right)\) và \(g\left( x \right)\)
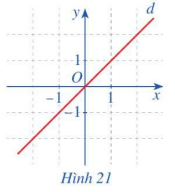
Quan sát đường thẳng d là đồ thị của hàm số \(g\left( x \right) = x\) (Hình 21) và cho biết gốc tọa độ O có là tâm đối xứng của đường thẳng d hãy không.
Hướng dẫn:
Dựa vào kiến thức về hàm số để xác định
Lời giải:
a)
Ta có: \(f\left( { – x} \right) = {\left( { – x} \right)^2} = {x^2},f\left( x \right) = {x^2} \Rightarrow f\left( { – x} \right) = f\left( x \right)\)
Trục đối xứng của (P) là đường thẳng y = 0
b)
Ta có: \(g\left( { – x} \right) = – g\left( x \right)\)
Gốc tọa độ O là tâm đối xứng của đường thẳng d