Áp dụng công thức tính thể tích khối chóp: \(S = \frac{1}{3}Bh\). Trong đó: \(B\) là diện tích đa giác đáy \(h\. Giải chi tiết Giải bài 7.34 trang 41 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài 27. Thể tích. Cho khối chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\…
Đề bài/câu hỏi:
Cho khối chóp đều \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng \(a\), góc giữa mặt phẳng \(\left( {SCD} \right)\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \(60^\circ \). Tính theo \(a\) thể tích khối chóp \(S.ABCD\).
Hướng dẫn:
Áp dụng công thức tính thể tích khối chóp: \(S = \frac{1}{3}Bh\).
Trong đó: \(B\) là diện tích đa giác đáy
\(h\)là đường cao của hình chóp
Bước 1: Xác định chiều cao \(SO\)
Bước 2: Tính diện tích đáy
Bước 3: Tính thể tích khối chóp \(V = \frac{1}{3}SO.{S_{ABCD}}\).
Lời giải:
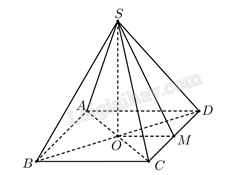
Gọi \(O\) là giao điểm của \(AC\) và \(BD\), ta có \(SO\) vuông góc với mặt đáy \(\left( {ABCD} \right)\). Kẻ \(OM\) vuông góc với \(CD\) tại \(M\) thì \(SM\) cũng vuông góc với \(CD\) nên góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng góc giữa hai đường thẳng \(SM\) và \(OM\), mà \(\left( {SM,OM} \right) = \widehat {SMO} = 60^\circ \). Ta có: \(OM = \frac{a}{2};\)\(SO = OM \cdot {\rm{tan}}\widehat {SMO} = \frac{{a\sqrt 3 }}{4}\). Vậy \({V_{S.ABCD}} = \frac{1}{3} \cdot {S_{ABCD}} \cdot SO = \frac{1}{3} \cdot {a^2} \cdot \frac{{a\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{12}}\).