Vẽ hình minh họa Gọi \(AB\) là giao tuyến của mặt phẳng mái nhà và mặt phẳng nằm ngang, \(AD\. Giải và trình bày phương pháp giải Giải bài 7.32 trang 38 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài 26. Khoảng cách. Trên một mái nhà nghiêng \({30^ \circ }\) so với mặt phẳng nằm ngang,…
Đề bài/câu hỏi:
Trên một mái nhà nghiêng \({30^ \circ }\) so với mặt phẳng nằm ngang, người ta dựng một chiếc cột vuông góc với mái nhà. Hỏi chiếc cột tạo với mặt phẳng nằm ngang một góc bao nhiêu độ? Vì sao?
Hướng dẫn:
Vẽ hình minh họa
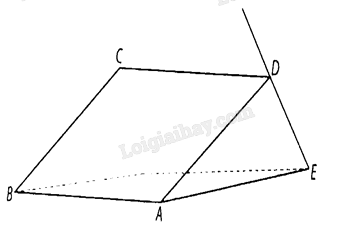
Gọi \(AB\) là giao tuyến của mặt phẳng mái nhà và mặt phẳng nằm ngang, \(AD\) là đường thẳng nằm trên mái nhà và vuông góc với \(AB\),
\(DE\) là chiếc cột vuông góc với mái nhà,
\(AE\) nằm trên mặt phẳng nằm ngang, khi đó tam giác \(ADE\) vuông tại \(D\), đường thẳng \(AE\) là hình chiếu vuông góc của \(DE\) trên mặt phẳng nằm ngang
Tính góc \(\widehat {DEA}\)
Lời giải:
Gọi \(AB\) là giao tuyến của mặt phẳng mái nhà và mặt phẳng nằm ngang, \(AD\) là đường thẳng nằm trên mái nhà và vuông góc với \(AB\), đường thẳng \(DE\) là chiếc cột vuông góc với mái nhà, đường thẳng \(AE\) nằm trên mặt phẳng nằm ngang, khi đó tam giác \(ADE\) vuông tại \(D\), đường thẳng \(AE\) là hình chiếu vuông góc của \(DE\) trên mặt phẳng nằm ngang, mà góc \(\widehat {DAE}\) bằng \({30^ \circ }\) nên góc giữa hai đường thẳng \(DE\) và \(AE\) bằng \({60^ \circ }\).
Vậy góc giữa đường thẳng \(DE\) (chiếc cột) và mặt phẳng nằm ngang bằng góc giữa hai đường \(DE\) và \(AE\) bằng \({60^ \circ }\)
