Sử dụng kiến thức về tính chất của hai mặt phẳng song song để chứng minh. Gợi ý giải Giải bài 6 trang 134 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài tập cuối chương 4. Cho hình chóp S. ABCD, đáy ABCD là hình thang có đáy lớn AB và \(AD = a\)….
Đề bài/câu hỏi:
Cho hình chóp S. ABCD, đáy ABCD là hình thang có đáy lớn AB và \(AD = a\). Mặt bên SAB là tam giác cân tại S, \(SA = a\); mặt phẳng (R) song song với (SAB) và cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q.
a) Chứng minh MNPQ là hình thang cân.
b) Đặt \(x = AM\) với \(0 < x < a\). Tính MQ theo a và x.
Hướng dẫn:
Sử dụng kiến thức về tính chất của hai mặt phẳng song song để chứng minh: Cho hai mặt phẳng (P) và (Q) song song với nhau. Nếu mặt phẳng (R) cắt (P) thì cắt (Q) và hai giao tuyến của chúng song song với nhau.
Lời giải:
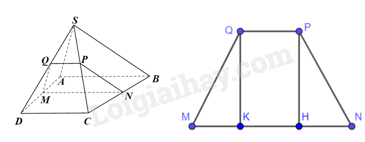
Ta có: Giao tuyến của mặt phẳng (ABCD) và (R) là MN, giao tuyến của mặt phẳng (ABCD) và (SAB) là AB. Mà (R)//(SAB) nên MN//AB.
Chứng minh tương tự ta có: các mặt phẳng (SAD), (SCB), (SCD) cắt hai mặt phẳng song song (R) và (SAB) theo các cặp giao tuyến song song.
Suy ra: MQ//SA, NP//SB, QP//CD//AB.
Do đó, MN//PQ nên tứ giác MNPQ là hình thang.
Ta có: \(\frac{{MQ}}{{SA}} = \frac{{DM}}{{DA}} = \frac{{CN}}{{CB}} = \frac{{NP}}{{SB}}\) (hệ quả định lí Thalès) và \(SA = SB \Rightarrow MQ = NP\)
Kẻ QK vuông góc với MN tại K, PH vuông góc với MN tại H.
Chứng minh được \(\Delta MKQ = \Delta NHP\left( {ch – cgv} \right) \Rightarrow \widehat {QMK} = \widehat {PNH}\)
Do đó, hình thang MNPQ là hình thang cân.
b) Ta có: \(\frac{{MQ}}{{SA}} = \frac{{DM}}{{DA}} \Rightarrow \frac{{MQ}}{a} = \frac{{a – x}}{a} \Rightarrow MQ = a – x\)