Sử dụng kiến thức về số trung bình của mẫu số liệu ghép nhóm để tính. Gợi ý giải Giải bài 1 trang 149 sách bài tập toán 11 – Chân trời sáng tạo tập 1 – Bài 1. Số trung bình và mốt của mẫu số liệu ghép nhóm. Nhân ngày hội đọc sách, các học sinh của một trường trung học phổ thông mang sách cũ đến tặng…
Đề bài/câu hỏi:
Nhân ngày hội đọc sách, các học sinh của một trường trung học phổ thông mang sách cũ đến tặng thư viện trường và trao đổi với các bạn học sinh khác. Bảng sau thống kê số sách cũ mà các bạn học sinh lớp 11B mang đến trường.

Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Hướng dẫn:
+ Sử dụng kiến thức về số trung bình của mẫu số liệu ghép nhóm để tính:
Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
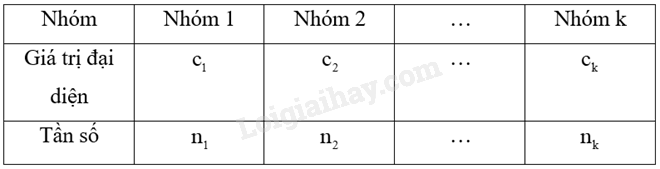
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + … + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + … + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} – {n_{m – 1}}}}{{\left( {{n_m} – {n_{m – 1}}} \right) + \left( {{n_m} – {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} – {u_m}} \right)\)
Lời giải:
Ta hiệu chỉnh bảng tần số ghép nhóm bao gồm các giá trị đại diện của nhóm là:

Số trung bình của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{2.5 + 5.14 + 8.10 + 11.8 + 14.3}}{{5 + 14 + 10 + 8 + 3}} = 7,25\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {3,5;6,5} \right)\).
Do đó, \({u_m} = 3,5;{n_{m – 1}} = 5;{n_m} = 14,{n_{m + 1}} = 10,{u_{m + 1}} – {u_m} = 6,5 – 3,5 = 3\)
Mốt của mẫu số liệu ghép nhóm là: \({M_O} = 3,5 + \frac{{14 – 5}}{{\left( {14 – 5} \right) + \left( {14 – 10} \right)}}.3 = \frac{{145}}{{26}}\)